if x = arccsc(sqrt(2)), this means that:
csc(x) = sqrt(2).
since csc(x) = 1/sin(x),this means that:
1/sin(x) = sqrt(2).
multiply both sides of this equation by sin(x) and divide both sides of this equation by sqrt(2) to get:
sin(x) = 1/sqrt(2).
multiply the expression on the right side of the equation by sqrt(2)/sqrt(2) to get:
sin(x) = sqrt(2)/2.
you can either recognize this as 45 degrees or you can use your calculator to see that this is 45 degrees.
that would be the value of this angle in the first quadrant.
since the sine of an angle is positive in the first quadrant and the second quadrant, then the angle whose sine is sqrt(2)/2 can be either 45 degrees or 180 - 45 degrees which equals 135 degrees.
you can use your calculator to verify that the sine of 45 degrees and the sine of 135 degrees are both equal to sqrt(2)/2.
you can also use your calculator to verify that the cosecant of 45 degrees and the cosecant of 45 degrees are both equal to sqt(2).
use your calculator to get sin(45) and the answer will be .7071067812
use your calculator to calculate sqrt(2)/2 and the answer will be .7071067812
in other words, sqrt(2)/2 and.7071067812 are equivalent.
use your calculator to get sin(135) and the answer will be .7071067812
in other words, sin(45) = sin(135).
to find cosecant(45), you need to get sin(45) and then take the reciprocal of it.
you get the reciprocal of it by dividing 1 by .7071067812 to get 1.414213562
use your calculator to get sqrt(2) and the answer will be 1.414213562
in other words 1.414213562 and sqrt(2) are equivalent.
your answer is:
theta equals arccsc (sqrt(2)) if and only if arccsc(theta) = sqrt(2).
this happens when theta equals 45 degrees and theta equals 135 degrees.
this assumes that your domain is all angles from 0 to 360.
if there is no restrictions on the domain, then the answer is answer is:
45 degrees plus or minus 360 degrees and 135 degrees plus or minus 360 degrees.
you can graph the equation of y = csc(x).
since you can't do that directly, then you need to graph the equation of y = 1/sin(x).
since most graphing software graphs trigonometric functions in radians, you need to convert 45 degrees and 135 degrees to radians.
the following graph shows you the graph of y = csc(x).
a horizontal line has been drawn at y = sqrt(2).
vertical lines have been drawn at the radian equivalent of x = 45, 135, 45 + 360 = 405, 135 + 360 = 495, 45 - 360 = -315, and 135 - 360 = -225 to show you that the the graph of y = csc(x) equals sqrt(2) when x equals those values.
please note that the graph of y = csc(x) and the graph of y = 1/sin(x) are the same.
-----
45 - 360 degrees = pi/4 - 2*pi radians = - (7/4)*pi radians = - 5.5 radians
45 degrees = pi/4 radians = .8 radians.
45 + 360 degrees = pi/4 + 2*pi radians = (9/4)*pi radians = 7.1 radians.
-----
135 - 360 degrees = (3/4)*pi - 2*pi radians = - (5/4)*pi radians = -3.9 radians.
135 degrees = (3/4)*pi radians = 2.356194 radians
135 + 360 degrees = (3/4)*pi + 2*pi radians = + (11/4)*pi radians = 8.6 radians.
-----
the graph will show vertical lines at these points and a horizontal line at y = sqrt(2).
the intersection of these vertical lines and the horizontal line will also intersect the graph of the equation of y = csc(x) which means that the value of csc(x) will be the y values indicated for the x values indicated.
the table used to plot these vertical lines is shown below:
x value y value degree equivalent of radians shown under x value
-5.5 1.414 -315 degrees (45 - 360)
0.8 1.414 45 degrees
7.1 1.414 405 degrees (45 + 360)
---
-3.9 1.414 -225 degrees (135 - 360)
2.4 1.414 135 degrees
8.6 1.414 495 degrees (135 + 360)
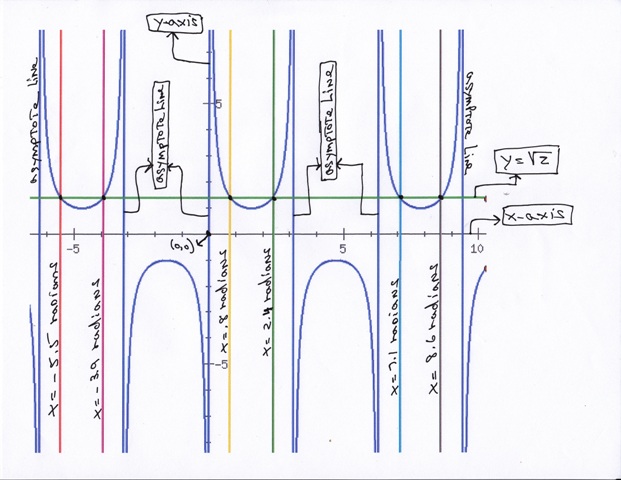
since degrees are cyclical, the graph goes on endlessly in both directions which is the reason why the domain of x must be specified for an interval unless you actually want to go on endlessly in both directions.