Question 416950: Please help with this problem.
1) As a science project, Anwar monitored the content of carbon monoxide outside his house in the city over several days. He found that it reached a maximum of about 30 ppm (parts per million) at 6:00 P.M., and a minimum of 10 ppm at 6:00 A.M.
a) Model the concentration of carbon monoxide, C, in parts per million, as a function of time, t, in hours. Use a sinusoidal function.
Found 2 solutions by stanbon, htmentor:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! Please help with this problem.
1) As a science project, Anwar monitored the content of carbon monoxide outside his house in the city over several days. He found that it reached a maximum of about 30 ppm (parts per million) at 6:00 P.M., and a minimum of 10 ppm at 6:00 A.M.
a) Model the concentration of carbon monoxide, C, in parts per million, as a function of time, t, in hours. Use a sinusoidal function.
----
amplitude = (30-10)/2 = 10
-----
Period = 24 hrs
So, (2pi)/b = 24
b = (1/12)pi
-------
Phase shift = ?
The day begins at 12:00PM which is 6hrs before max.
So, -c/b = 6 hrs
So, -c/[1/12pi] = 6
-c = (1/2)pi
c = -(pi/2)
=====================
Equation:
y = 10sin[(2pi/9)x-(pi/2)]+20
----
=====================
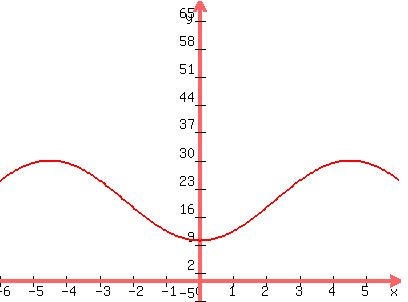
Cheers,
Stan H.
Answer by htmentor(1343)  (Show Source):
|
|
|
