Question 212798: write an equation of the sine function with amplitude 3,period 3pi/2, and phase shift pi/4
a)y=3sin(3x/2 - pi/4)
b)y=-3sin(4x/3 - pi/4)
c)y=-3sin(3x/2 - 3pi/8)
d)y=3sin(4x/3 - pi/3)
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! write an equation of the sine function with amplitude 3,period 3pi/2, and phase shift pi/4
a)y=3sin(3x/2 - pi/4)
b)y=-3sin(4x/3 - pi/4)
c)y=-3sin(3x/2 - 3pi/8)
d)y=3sin(4x/3 - pi/3)
 , with B and C positive.
has amplitude , with B and C positive.
has amplitude  , period , period 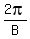 , and phase shift , and phase shift 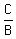 ,
The shift is right if ,
The shift is right if  is positive and left if is positive and left if  is negative.
We'll test each possible answer:
a)
is negative.
We'll test each possible answer:
a) has amplitude
has amplitude  ,
period ,
period  and phase shift
and phase shift  .
b) .
b) has amplitude
has amplitude  ,
period ,
period  and phase shift
and phase shift  .
c) .
c) has amplitude
has amplitude  ,
period ,
period  and phase shift
and phase shift  .
d) .
d) has amplitude
has amplitude  ,
period ,
period  and phase shift
and phase shift  So (d) is the only correct choice.
Edwin
So (d) is the only correct choice.
Edwin
|
|
|