Question 205950: how do you find the domain and range of these without a calculator?
y=2sinx
y=secx+2
y=sin|x|
ln(x-2)
Answer by mickclns(59)   (Show Source): (Show Source):
You can put this solution on YOUR website! y=2sinx
sinx goes back and forth between -1 and 1, so the domain is all real numbers (there is no real number that you cannot take the sine of) and the range is all real numbers between -1 and 1, inclusive. The domain of 2sinx is the same as the domain of sinx, but every y value of 2sinx is stretchedtwice as far away from the x-axis as that of sinx so, the range of 2sinx is all real numbers between -2 and 2, inclusive.
y = secx + 2
secx is 1/cosx
cosx goes back and forth between -1 and 1, so secx is 1 divided by numbers between 0 and 1 and between -1 and 0. When cosx is 0, then secx is undefined (has no value) so those are the values that are not in the domain, that is 90 + 180k degrees where k is any integer which is the same as pi/2 + pi(k) radians (the units usually used for all but most basic trig. Since adding 2 to secx doesn't change which values of x work in the function, the domain for secx + 2 is all real numbers except those of the form
pi/2 + pi(k) for k an integer.
Since secx is 1 divided by numbers between 0 and 1 and between -1 and 0, the range of secx is all real numbers that are greater than or equal to 1 or less than or equal to -1. Since adding 2 to secx moves everything up 2, the range of secx + 2 is all real numbers that are greater than or equal to 3 or less than or equal to +1.
sin|x|
The graph of this looks like this 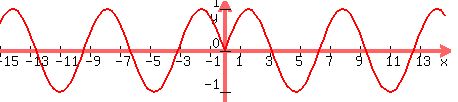
Any time you take an equation and replace x by |x|, the effect on the graph is as follows:
To the right of the y-axis, the graph is unchanged. To the left of the y-axis, the graph is replaced by the reflection of the right side of the graph over the y-axis (so it becomes symmetric about the y-axis.
The domain and range of sin|x| are going to be the same as that of sinx (see first part of first problem).
ln(x-2)
You can take a natural log of any positive number, but not of 0 or of a negative number, so the domain of lnx is all positive real numbers. When you take lnx where x is a tiny positive number, say 1/ (e^100) you get a large negative, in this case, -100. If you want lnx to have a large positive value, say 100, then x must be e^100... in other words ln(e^100) = 100, BUT, lnx can have the value of ANY positive number, just use a relatively huge number for x. This is to say that the range of lnx is all real numbers. The effect on the graph of replacing x with x-2 in an equation is moving everything to the right 2. This in itself has no effect on the range, but may have an effect on the domain. In this case, the domain of ln(x-2) is all real numbers (strictly) greater than 2 and the range is all real numbers. Here is a graph of the two functions:

|
|
|