Question 204635: hi i am really having trouble with converting rectangular coordinates to polar coordinates because i first have to graph the points and find four different ways to express those points with differing angles.
the points that i am having trouble with are (-10,-10)
Found 2 solutions by Alan3354, Edwin McCravy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! hi i am really having trouble with converting rectangular coordinates to polar coordinates because i first have to graph the points and find four different ways to express those points with differing angles.
the points that i am having trouble with are (-10,-10)
---------------
The radius, r, is sqrt(x^2 + y^2)
r = sqrt(200) = 10sqrt(2)
-----------------------
(-10,-10) is in quadrant 3.
The tan of the angle is y/x = 1
angle = 225º
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website! hi i am really having trouble with converting rectangular coordinates to polar coordinates because i first have to graph the points and find four different ways to express those points with differing angles.
the points that i am having trouble with are (-10,-10)
Let's plot the point (x,y) = (-10,-10):
 Now let's draw in
Now let's draw in  , ,  , and r, which we
will calculate: , and r, which we
will calculate:
 We calculate r by the Pythagorean theorm
We calculate r by the Pythagorean theorm







 The reference angle is 45°, indicated by the red arc below:
The reference angle is 45°, indicated by the red arc below:
 So the angle in standard position, indicated by the blue arc
below is 180°+45° or q = 225°, or
So the angle in standard position, indicated by the blue arc
below is 180°+45° or q = 225°, or  in radians: in radians:
 So one way to express the rectangular point
(x,y) = (-10,-10)
in polar form is
(r,q) = (
So one way to express the rectangular point
(x,y) = (-10,-10)
in polar form is
(r,q) = (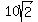  or if you want q in radian measure
(r,q) = ( or if you want q in radian measure
(r,q) = (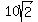 , , )
----
Another angle in standard position, indicated by the green arc
below is -180°+45° = -135° or )
----
Another angle in standard position, indicated by the green arc
below is -180°+45° = -135° or 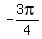
 So another way to express the rectangular
point (x,y) = (-10,-10) in polar form is
(r,q) = (
So another way to express the rectangular
point (x,y) = (-10,-10) in polar form is
(r,q) = (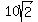  or if you want q in radian measure
(r,q) = ( or if you want q in radian measure
(r,q) = (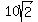 , ,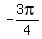 )
To find a third one, just add 360° or )
To find a third one, just add 360° or  to the positive angle.
(r,q) = ( to the positive angle.
(r,q) = (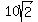  or if you want q in radian measure
(r,q) = ( or if you want q in radian measure
(r,q) = (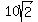 , ,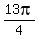 )
---
To find a fourth one, just add -360° or )
---
To find a fourth one, just add -360° or 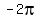 to the negative angle.
(r,q) = ( to the negative angle.
(r,q) = (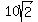  or if you want q in radian measure
(r,q) = ( or if you want q in radian measure
(r,q) = (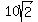 , , )
Edwin )
Edwin
|
|
|