There are infinitely many asymptotes for each of
these.
Rules:
To find asymptotes for
Tangent and secant graphs
Set the argument (what the tangent or secant is of)
equal to 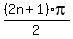 and solve for x.
Then let n = any integer, positive, negative, or zero.
Cotangent and cosecant graphs
Set the argument (what the cotangent or cosecant is of)
equal to
and solve for x.
Then let n = any integer, positive, negative, or zero.
Cotangent and cosecant graphs
Set the argument (what the cotangent or cosecant is of)
equal to 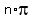 and solve for x.
Then let n = any integer, positive, negative, or zero.
[Note: the asymptotes are not affected by a coefficient
in front of the trig function]
------------------------------------------
and solve for x.
Then let n = any integer, positive, negative, or zero.
[Note: the asymptotes are not affected by a coefficient
in front of the trig function]
------------------------------------------
1. What are the asymptotes of 
This is a cotangent graph, so set
 Remove the decimal by multiplying both sides by 10
Remove the decimal by multiplying both sides by 10


 Let n = -3, -2, -1, 0, 1, 2, 3
Let n = -3, -2, -1, 0, 1, 2, 3
 ,
, ,
,  ,
, ,
,  ,
,  ,
,  , etc., etc.,
This becomes:
, etc., etc.,
This becomes:
 ,
, ,
,  ,
, ,
,  ,
,  ,
,  , etc., etc.,
These are all asymptotes.
-------------------------------
, etc., etc.,
These are all asymptotes.
-------------------------------
2. What are the asymptotes of 
This is a secant graph, so set



 Let n = -3, -2, -1, 0, 1, 2, 3
Let n = -3, -2, -1, 0, 1, 2, 3
 ,
, ,
, ,
, ,
, ,
, ,
, This becomes:
This becomes:
 ,
, ,
,  ,
, ,
,  ,
,  ,
,  , etc., etc.,
These are all asymptotes.
-------------------
, etc., etc.,
These are all asymptotes.
-------------------
3. What are the asymptotes of 
Note: The  in front does not affect the asymptotes,
This is a cosecant graph, so set
in front does not affect the asymptotes,
This is a cosecant graph, so set
 Let n = -3, -2, -1, 0, 1, 2, 3
Let n = -3, -2, -1, 0, 1, 2, 3
 ,
, ,
,  ,
, ,
,  ,
,  , x = 3pi, etc., etc.,
These are all asymptotes.
Edwin
, x = 3pi, etc., etc.,
These are all asymptotes.
Edwin