Question 170144: I'm attempting to do corrections on a test, but these three questions are giving me trouble! I've tried several different things, and I keep coming up with the same (wrong!) answer!
1) If  is an angle in quadrant 4 and is an angle in quadrant 4 and  , find the value of , find the value of 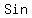   . .
2) What is the solution set of the equation
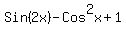 = = 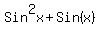 in the interval in the interval  ? ?
3) Find the solution set of  over the domain over the domain 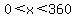 °. °.
Found 2 solutions by stanbon, Edwin McCravy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) If x is an angle in quadrant 4 and cotx= -7/24, find the value of
sin[(1/2)x].
If cotx = -7/24, x = 7 and y = -24
Then r = sqrt(7^2 + 24^2) = 25
------------
sin[(1/2)x] = sqrt[(1-cos(x))/2]
So, sin[(1/2)x] = sqrt[(1-(7/25))/2] = sqrt[9/25] = 3/5
=============================================================
2) What is the solution set of the equation sin(2x)-cos^2(x+1) = sin^2(x)+sinx in the interval 0
Comment: That is a mess to analyze. Graph the left side and the right side
separagely and see where they intersect under the condition the 0
=============================================================
3) Find the solution set of 6sinx + 11= 2cscx over the domain 0
Multiply thru by sin(x) to get:
6sin^2(x) + 11sin(x) - 2 = 0
---
Let w = sin(x)
Substitute to get:
6w^2 + 11w - 2 = 0
6w^2 +12w - w -2= 0
6w(w+2) -(w+2) = 0
(w+2)(6w-1) = 0
w = -2 or w = 1/6
-----
Solve for x:
sin(x) = -2 or sin(x)= 1/6
sin(x) cannot be -2.
If sin(x) = 1/6, x = 9.594.. degrees or 170.41 degrees
========================================================
Cheers,
Stan H.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! Stanbon's solution is correct but he does not do problem 2 and he does not explain why we know to take the positive square root in 1.
Edwin's solution:
1) If  is an angle in quadrant 4 and is an angle in quadrant 4 and  , find the value of , find the value of 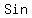   .
Since this involves drawing a graph in which .
Since this involves drawing a graph in which  represents
the horizontal axis, not an angle, I will temporarily change represents
the horizontal axis, not an angle, I will temporarily change
 to to 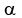 to avoid a conflict of letters. Change
the problem to read this way:
1) If to avoid a conflict of letters. Change
the problem to read this way:
1) If  is an angle in quadrant 4 and is an angle in quadrant 4 and  , find the value of , find the value of 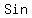   .
We must use the identity: .
We must use the identity:
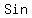     However we do not know
However we do not know 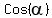 So we must first draw the picture of the angle
So we must first draw the picture of the angle  :
We know that :
We know that 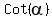 is by definition is by definition  , we
can draw the angle in the 4th quadrant with referent angle
is inside a triangle whose horizontal side , we
can draw the angle in the 4th quadrant with referent angle
is inside a triangle whose horizontal side  is taken
to be the numerator of is taken
to be the numerator of 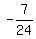 , considered positive because
it goes right of the y-axis, and whose vertical side , considered positive because
it goes right of the y-axis, and whose vertical side  is taken as
the denominator is taken as
the denominator  , taken negative because it goes down
below the x-axis: , taken negative because it goes down
below the x-axis:
 Next we calculate
Next we calculate  by the Pythagorean theorem: by the Pythagorean theorem:





 So we label the slanted line segment
So we label the slanted line segment  . .
 Now we can find
Now we can find 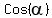
 So we substitute
So we substitute  for for 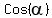 in in
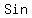    
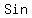    
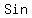    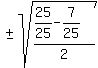
    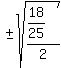
    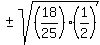
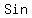    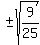
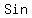    ± ± Next we must decide whether this is positive or negative:
Since
Next we must decide whether this is positive or negative:
Since  is is the 4th quadrant, then is is the 4th quadrant, then
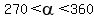 ° so multiplying that through by ° so multiplying that through by 
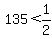 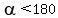 °
The means °
The means   is in quadrant 2. Since
the sine is positive in the 2nd quadrant, the final answer
is is in quadrant 2. Since
the sine is positive in the 2nd quadrant, the final answer
is
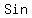   And of course now that we have the answer we can change
And of course now that we have the answer we can change
 back to back to  : :
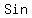   2) What is the solution set of the equation
2) What is the solution set of the equation
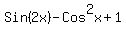 = = 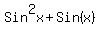 in the interval in the interval  ?
Use the identity ?
Use the identity  to replace to replace 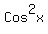 on the
left side: on the
left side:
 = = 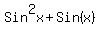
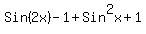 = = 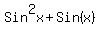
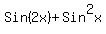 = = 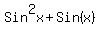
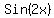 = = 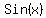
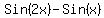 = =  Now use identity
Now use identity  to
replace to
replace 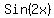
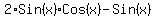 = =  Factor out
Factor out 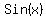
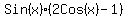 = =  Use the zero-factor principle:
Use the zero-factor principle:
 3) Find the solution set of
3) Find the solution set of  over the domain over the domain 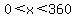 °. °.
 Use identity
Use identity 
 Multiply through by
Multiply through by 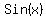


 Use the zero-factor principle:
Use the zero-factor principle:
 Edwin
Edwin
|
|
|