Question 132404: Four 6-by-6 squares are drawn on a rhombus having two 30 degree angles. Find the area of the fifth square that is formed by connecting the centers of the squares.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
In the above diagram, the blue figure is the given rhombus, the green squares are two of the constructed squares, and the red line connecting the centers of these two squares must be a diagonal of the desired square. Since a diagonal of a square is in proportion to its sides by a factor of  , we only need find the length of this diagonal to be able to compute the length of one of the sides of the desired square. , we only need find the length of this diagonal to be able to compute the length of one of the sides of the desired square.
The coordinates of the vertices of the rhombus are:
(0,0),
(6,0),
(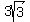 ,3), and ,3), and
(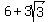 ,3) ,3)
That means the lower square must have vertices at:
(0,0),
(6,0),
(6,-6), and
(0,-6)
Therefore the lower square must have a center at the mid-point of a diagonal, (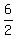 , ,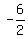 ), or (3,-3) ), or (3,-3)
And the upper square:
(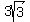 ,3), ,3),
(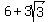 ,3), ,3),
(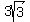 ,9), and ,9), and
(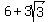 ,3) ,3)
Therefore the upper square must have a center at (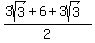 , ,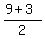 ), or ( ), or ( ,6) ,6)
The distance from ( ,6) to (3,-3) is given by the distance formula: ,6) to (3,-3) is given by the distance formula:





The diagonal of a square forms an isoceles right triangle with two adjacent sides, and the sides of an isoceles right triangle are in proportion to the hypotenuse as  :1. So, just take the length of the diagonal and multiply by :1. So, just take the length of the diagonal and multiply by  . .
 is the length of a side of the desired square. Therefore the area of the desired square is is the length of a side of the desired square. Therefore the area of the desired square is  square units. square units.
|
|
|