SOLUTION: on the same set of axes, sketch and label the graphs of the equations y= 2 cos 2x and y = -2 sin x in the interval 0 <u><</u> x <u><</u> {{{pi}}} find the values which 2 cos 2x =

Algebra ->  Trigonometry-basics -> SOLUTION: on the same set of axes, sketch and label the graphs of the equations y= 2 cos 2x and y = -2 sin x in the interval 0 <u><</u> x <u><</u> {{{pi}}} find the values which 2 cos 2x =      Log On


   

Question 130107: on the same set of axes, sketch and label the graphs of the equations y= 2 cos 2x and y = -2 sin x in the interval 0 < x < pi
find the values which 2 cos 2x = -2 sin x
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!


On the same set of axes, sketch and label the 

graphs of the equations



y = 2cos(2x) 



and 



y = -2sin(x) 



in the interval 0 < x < pi.



find the values which 2 cos 2x = -2 sin x



The rule for the graphs of:



y = Asin(Bx) and y = Acos(Bx)



both have these important points on the x-axis:



0, ±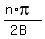%28n%2Api%29%2F%282B%29 where n is any integer.



The peaks all have y-coordinate |A|.

The valleys all have y-coordinates -|A|



If A is positive,

y = Asin(Bx) circulates from x-intercept at the origin, peak, x-intercept, valley, x-intercept, peak, etc. 



y = Acos(Bx) circulates from a peak at the origin, x-intercept, valley, x-intercept, peak, etc.



Peaks and valleys in the rules above reverse if A is negative.



So for y = 2cos(2x)



A = 2, B = 2.  This graph has important points at 



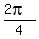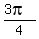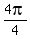
x = 0, pi%2F4, %282pi%29%2F4, %283pi%29%2F4, 4pi%2F4 



which simplify to 



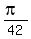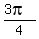x = 0, pi%2F4, %28pi%29%2F42, %283pi%29%2F4, pi   



It has 

a peak at (0,2), 

an x-intercept at (pi%2F4,0),

a valley at (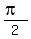%28pi%29%2F2,-2),

an x-intercept at (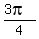%283pi%29%2F4,0),

and a peak at (pi,2)



This is the graph:







Now for y = -2sin(x)



A = -2, B = 1.  This graph has important points at 



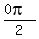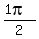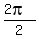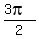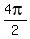
x = %280pi%29%2F2, %281pi%29%2F2, %282pi%29%2F2, %283pi%29%2F2, 4pi%2F2 



which simplify to 



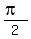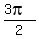x = 0, %28pi%29%2F2, pi, %283pi%29%2F2, 2pi



but only the first three are within the interval 0 < x < pi  



Since A is negative, the peaks and valleys switch from the 

rules above and there are only these on the interval 0 < x < pi



an x-intercept at (0,0),

a valley at (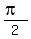%28pi%29%2F2,-2),

an x-intercept at (pi,0)



This is the graph (it only has one arch on this

interval 0 < x < pi.







Now let's put them both on the same set of axes:







To find the solution of



2 cos 2x = -2 sin x



we just observe that the solution will be the x-coordinate of

the point where the two curves intersect.



Well it looks as though they intersect only at one point,

which is (pi%2F2,-2), their common valley point.



So the solution in the interval 0 < x < 2pi is x = pi%2F2



Edwin