SOLUTION: Solve sin x + cos x = 1 for x.

We start from

    sin x + cos x = 1 for x.    (1)


Square both sides

    sin^2(x) + cos^2(x) + 2*sin(x)*cos(x) = 1.


Replace sin^2(x) + cos^2(x) by 1  (according the Pythagorean theorem)

    1 + 2*sin(x)*cos(x) = 1.


Cancel "1" in both sides and write in the form

    sin(2x) = 0.


Hence,  2x = .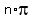


It implies  x = 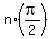,   n = 0, +/-1, +/-2, . . .    (2)


We squared the original equation - so, erroneous and excessive roots could arise.
Therefore, we should check the roots (2).


Checking shows that only  x  with  n = 4k  and  n = 4k+1  satisfy the original equation.


It gives the ANSWER :  the solutions are  x =   and  x = 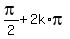,  k = 0, +/-1, +/-2, . . .