SOLUTION: Find (1 - i)4. Show your work using DeMoivre’s Theorem.

Actually, you want to find  (1-i)^4 =   using DeMoivre’s formula.


So, you start from complex number z = 1-i.


It has the modulus of   = sqrt(2) 

and the argument 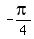 ,  so we can write it in this "cis"-form  z = .


Then, according to the deMoivre's formula

     =  =  = 4*(-1) = -4.


ANSWER.   = -4.