SOLUTION: Hi, I am struggling with this problem. Thanks. {{{"sin"^2x + (1)/("sin"^2x) + "sin x" + (1)/("sin x") = 4}}}

Algebra ->  Trigonometry-basics -> SOLUTION: Hi, I am struggling with this problem. Thanks. {{{"sin"^2x + (1)/("sin"^2x) + "sin x" + (1)/("sin x") = 4}}}      Log On


   

Question 1204440: Hi, I am struggling with this problem. Thanks.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Let w+=+sin%28x%29

The original equation that your teacher gave you turns into w%5E2+%2B+1%2F%28w%5E2%29+%2B+w+%2B+1%2Fw+=+4

Multiply both sides by the LCD w^2 to clear out the fractions.
w%5E2+%2B+1%2F%28w%5E2%29+%2B+w+%2B+1%2Fw+=+4
w%5E2%28w%5E2+%2B+1%2F%28w%5E2%29+%2B+w+%2B+1%2Fw%29+=+4w%5E2
w%5E4+%2B+1+%2B+w%5E3+%2B+w+=+4w%5E2
w%5E4+%2B+w%5E3+%2B+w+%2B+1+=+4w%5E2
w%5E4+%2B+w%5E3+%2B+w+%2B+1-4w%5E2+=+0
w%5E4+%2B+w%5E3+-+4w%5E2+%2B+w+%2B+1+=+0
Use the rational root theorem to check the factors of the last term (1)
The possible rational roots would be: 1 or -1
Plug in w = -1 to get a nonzero result
But w = 1 would lead to zero, which shows w = 1 is a root.

The root w = 1 means w-1 is a factor of w^4 + w^3 - 4w^2 + w + 1

Use polynomial long division, or synthetic division, to find that

or simply
%28w%5E4+%2B+w%5E3+-+4w%5E2+%2B+w+%2B+1%29%2F%28w-1%29+=+w%5E3%2B2w%5E2-2w-1

Then notice how w = 1 is also a root of w^3+2w^2-2w-1 due to the rational root theorem.

w = 1 is a repeated root of w^4 + w^3 - 4w^2 + w + 1
So (w-1)^2 is a factor of w^4 + w^3 - 4w^2 + w + 1

Turns out that
w%5E4+%2B+w%5E3+-+4w%5E2+%2B+w+%2B+1
factors to
%28w-1%29%5E2%28w%5E2%2B3w%2B1%29
Polynomial long division can be used to find this.

From here, use the quadratic formula to solve w^2+3w+1 = 0
I'll skip steps.
The results are: w+=+%28-3%2Bsqrt%285%29%29%2F2 and w+=+%28-3-sqrt%285%29%29%2F2
They approximate to w = -2.618 and w = -0.382 respectively.



In summary so far:
The four roots of w^4 + w^3 - 4w^2 + w + 1 are
w = 1
w = 1
w = -2.618 (approximate)
w = -0.382 (approximate)

Recall we made w = sin(x)
w = 1 leads to sin(x) = 1 and this partial solution set:
x = pi/2 + 2pi*n
where n is an integer.
I'm assuming you are in radian mode.
If you are in degree mode, then replace pi/2 with 90 and replace 2pi with 360.

w = -2.618 does not lead to any real number solutions for x because the smallest sin(x) can get is -1.

w = -0.382 does lead to solutions for x since -0.382 is between -1 and 1.
I'll let you solve sin(x) = -0.382
There are two sub-branches here.

Answer by ikleyn(52906) About Me  (Show Source):
You can put this solution on YOUR website!
.
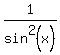sin%5E2%28x%29 + 1%2Fsin%5E2%28x%29 + sin(x) + 1%2Fsin%28x%29 = 4.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

Introduce new variable

    y = sin(x) + 1%2Fsin%28x%29.


Then y^2 = sin^2(x) + 2 + 1/sin^2(x),  and the original equation takes the form

    y^2 - 2 + y = 4,

or

    y^2 + y - 6 = 0.


Its roots are (using the quadratic formula)

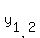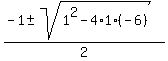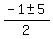    y%5B1%2C2%5D = %28-1+%2B-+sqrt+%281%5E2+-+4%2A1%2A%28-6%29%29%29%2F2 = %28-1+%2B-+sqrt%2825%29%29%2F2 = %28-1+%2B-+5%29%2F2,

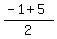    or  y%5B1%5D = %28-1%2B5%29%2F2 = 2,  y%5B2%5D = %28-1-5%29%2F2 = -3.


It means that  sin(x) + 1%2Fsin%28x%29  is  EITHER  2  OR  -3.


So, from this point, we have two cases for x.



(1)  sin(x) + 1%2Fsin%28x%29 = 2,  which implies

     sin^2(x) - 2sin(x) + 1 = 0,

     (sin(x) - 1)^2 = 0

      sin(x) = 1

          x  = 90 degrees (or  x = pi%2F2).

      Thus this case is complete.



(2)  sin(x) + 1%2Fsin%28x%29 = -3,  which implies

     sin^2(x) + 3*sin(x) + 1 = 0,

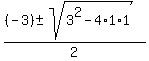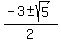     sin(x) = use the quadratic formula = %28%28-3%29+%2B-+sqrt+%283%5E2+-+4%2A1%2A1%29%29%2F2 = %28-3+%2B-+sqrt%285%29%29%2F2. 

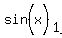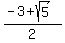     sin%28x%29%5B1_%5D = %28-3+%2B+sqrt%285%29%29%2F2 = ~ -0.382  --->  from it, you may find two values for x between 0 and 360 degrees.

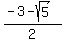     sin%28x%29%5B2_%5D = %28-3+-+sqrt%285%29%29%2F2 = ~ -2.618  --->  there is no solution for real x. 

      Thus this case is complete, too.

Solved.

-------------------

Comparing with the solution by tutor @math_tutor2020, the substitution which I used, leads
to equation/equations of degree 2, ONLY. There is no need to work with equation of degree 4.