.
Find the largest possible domain and largest possible range of the function
𝑔(𝑥) = 4 cos(3𝑥) − 3 sin(3𝑥).
Give your answers in set/interval notations.
~~~~~~~~~~~~~~~~~~~~~
The domain is, OBVIOUSLY, the set of all real numbers, since this function (this expression)
is defined over all this set.
To find the range, let's make this identical transformation
4*cos(3x) - 3*sin(3x) = 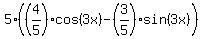 . (1)
Next, notice that
. (1)
Next, notice that  +
+ 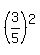 =
= 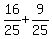 =
= 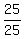 = 1.
THEREFORE, there is such angle
= 1.
THEREFORE, there is such angle  that
that  =
=  ,
,  =
=  .
This
.
This  is simply the angle in QI, which satisfies this equation
is simply the angle in QI, which satisfies this equation  =
=  , or
, or  =
=  .
Then we can continue the equality (1) this way
4*cos(3x) - 3*sin(3x) =
.
Then we can continue the equality (1) this way
4*cos(3x) - 3*sin(3x) = 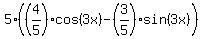 =
= 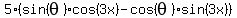 =
now apply the formula for sine of the sum of arguments
=
=
now apply the formula for sine of the sum of arguments
= 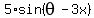 .
Thus we presented the original expression as the sine function with amplitude 5 of argument
.
Thus we presented the original expression as the sine function with amplitude 5 of argument 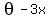 4*cos(3x) - 3*sin(3x) =
4*cos(3x) - 3*sin(3x) = 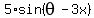 .
It tells you that the range of 4*cos(3x) - 3*sin(3x) is the interval from -5 to 5, or, in the interval form, [-5,5].
ANSWER. The domain of the given function is the entire number line (-oo,oo).
The range of the given function is the interval [-5,5].
.
It tells you that the range of 4*cos(3x) - 3*sin(3x) is the interval from -5 to 5, or, in the interval form, [-5,5].
ANSWER. The domain of the given function is the entire number line (-oo,oo).
The range of the given function is the interval [-5,5].
Solved.
----------------
This transformation and the logic, which I used, may seem as a focus - pocus.
But actually, it is a general transformation of the expression a*cos(x) - b*sin(x) with real coefficients "a" and "b"
into single harmonic function
a*sin(x) - b*cos(x) = 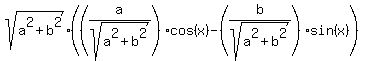 =
=
=
= 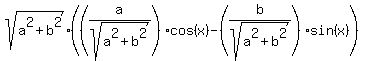 =
=
=
= 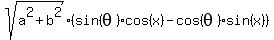 =
= 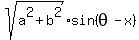 .
where
.
where  =
= 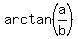 .
It works always for any real coefficients "a" and "b" and transforms any linear combination a*cos(x) + b*sin(x)
into single harmonic function
.
It works always for any real coefficients "a" and "b" and transforms any linear combination a*cos(x) + b*sin(x)
into single harmonic function 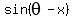 with the shift
with the shift  =
= 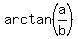 and the amplitude
and the amplitude  .
It is very useful classic trigonometric transformation and the identity to know and to use in different
trigonometric problems.
So, it makes sense to learn and to memorize it.
.
It is very useful classic trigonometric transformation and the identity to know and to use in different
trigonometric problems.
So, it makes sense to learn and to memorize it.