The identity to use is 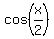

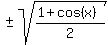 Since we are finding
Since we are finding 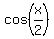 we divide all three sides of the domain for
x by 2, so we'll have the domain for
we divide all three sides of the domain for
x by 2, so we'll have the domain for  .
.
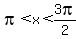 , divide through by 2:
, divide through by 2:
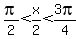 , which in degrees is between 90o and 135o.
which means x/2 is in QII. The cosine is negative in QII, so we use the
negative sign
, which in degrees is between 90o and 135o.
which means x/2 is in QII. The cosine is negative in QII, so we use the
negative sign
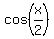

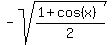
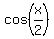


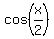

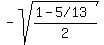 Multiply inside the square root radical by 13/13
Multiply inside the square root radical by 13/13
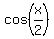


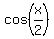

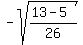
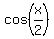

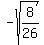
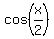

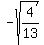
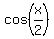

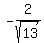 You can rationalize the denominator of that if you like.
Edwin
You can rationalize the denominator of that if you like.
Edwin