Question 1201900: Evaluate:
arccos[cos(-4pi/3)]
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! this appears to be in radians.
arccos(cos(-4pi/3)) = 2.094395102 radians.
simplest way to do it,if you don't know how to do it in one shot, is to find cos(-4pi/3) first and than find the arccos of that.
cos(-4pi/3) = -.5
arccos(-.5) = 2.094395102.
note that -4pi/3 is a negative angle.
to convert to a positive angle between 0 and 2pi radians, add 2pi radians to it until it goes positive.
you will get -4pi/3 + 2pi = 2.094395102 radians.
that is the an equivalent positive angle that has the same trig functions as the noriginal negative angle.
your expression then becomes:
arccos(cos(2.094395102)) = 2.094395102.
this is easier to see in degrees.
thd equivalent angle in degrees of -4pi/3 is equal to that * 180 / pi = -240 degrees.
the original expression then becomes arccos(cos(-240)).
the equivalent positive angle to -240 degrees is found by adding 360 to it until it becomes positive between 0 and 360 degrees.
-240 + 360 = 120 degrees.
the expression becomes arecos(cos(120)) degrees = 120 degrees.
cos(120) = -.5.
arccos -.5 = 120.
by equivalent angles, it is meant that they have the same trig function values.
trig functions for 120 degrees are:
sine = .8660254038
cosine = -.5
tangent = .1.732050808
trig functions for -240 degrees are:
sine = .8660254038
cosine = -.5
tangent = .1.732050808
note that the reference angle for 120 degrees is equal to 180 - 120 = 60 degrees.
note also that the reference angle for -240 degrees is the same, because -240 is equivalent to 120 degrees and the reference angle for 120 degrees is 60 degrees.
note also that sin(60) = .5 and cosinje(60) = sqrt(3)/2 which is equal to .8660254038.
your solution is that arccos(cos(-4pi/3)) = 2.094395102 radians.
Answer by ikleyn(52832)  (Show Source):
You can put this solution on YOUR website! .
Evaluate: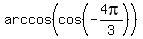 
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The angle 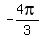 lies in the second quadrant, QII.
The cosine function of this angle has a negative value.
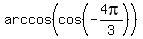They want you find the angle, , which has the same value of cosine as the angle  .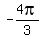
arccos is, BY THE DEFINITION, an angle in the range from 0 to  , [0,).
So, they want you find an angle in the range [0,), which has the same cosine value,
as 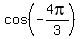 . It is the angle in the range [0,), which has the same projection on x-axis
as the angle 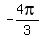. The desired angle is,  ,  .
Geometrically, it is the same angle as 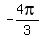, but this is expressed and presented in the right range.
This EXACT value is PRECISELY what they want from you. There is NO NEED to transform it to numerical value in radians.
You may transform it in radians for the sake of your curiosity, if you want, but in reality, it is NOT NEEDED.
This exact value, , is PRECISELY what they want from you.
ANSWER. = .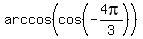
Solved, with all necessary explanations.
-----------------
In solution of this problem, the major step is to get a precise understanding
what they want from you, and formulate it clearly, as I did it in my post.
To understand my solution better, read and re-read it several times: as many times,
as you need to get FULL UNDERSTANDING.
I know that for beginner students, such problems are difficult and perplex them.
The only way to crawl into this area is to get it from an expert and read and re-read it as many times,
as it is needed for full understanding. There is NO OTHER WAY.
/////////////////
If you want to see other similar and different solved problems, look into the lesson
- Advanced problems on calculating trigonometric functions of angles
in this site.
|
|
|
