Question 1201677: PLEASE do GIVE CoRRECT AnSwers
1. Convert the rectangular form of the complex number 2-2i
into polar form. Show all work and label the modulus and argument.
2. Find all cube roots of the complex number 64(cos(219 degree) + i sin (219 degree)). Leave answers in polar form and show all work.
Found 3 solutions by math_tutor2020, greenestamps, ikleyn:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!
Edit: Sorry I had a brainfart. I mentioned the angle in Q2 when it should have been Q4.
I have fixed the mistake.
I'll do problem 1 to get you started.
2-2i = 2 + (-2)i
this is written in the form a+bi
a = 2
b = -2
r = modulus
r = sqrt(a^2+b^2)
r = sqrt((2)^2+(-2)^2)
r = sqrt(4+4)
r = sqrt(8)
r = sqrt(4*2)
r = sqrt(4)*sqrt(2)
r = 2*sqrt(2)
theta = argument
theta = arctan(b/a)
theta = arctan(-2/2)
theta = arctan(-1)
theta = -45°
Add 360 degrees to find a coterminal angle in the range 0 ≤ theta < 360
-45+360 = 315
Summary:
r = 2*sqrt(2)
theta = 315°
The polar point (r, theta) is (2*sqrt(2), 315°)
Another way you could express the answer would be to say the following
z = r*( cos(theta) + i*sin(theta) )
z = 2*sqrt(2)*( cos(315°) + i*sin(315°) )
z = 2*sqrt(2)*cis(315°)
where "cis" is shorthand for "cosine i sine"
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
1. Convert 2-2i to polar form
 , so the reference angle is 45 degrees, or pi/4 radians.
The given number has positive real part and negative imaginary part, so it is in quadrant IV. A 45 degree reference angle in quadrant IV is -45 degrees, or -pi/4 radians.
The modulus is  .
ANSWERS:
(2*sqrt(2),-pi/4) or (2*sqrt(2))cis(-pi/4)
modulus: 2*sqrt(2)
argument: -pi/4
Answer by ikleyn(52794)  (Show Source):
You can put this solution on YOUR website! .
The number 2-2i is located in 4th quadrant, QIV.
Its modulus is  =  =  =  .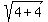
Its argument is -45° or 360°-45° = 315°.
(You may use any of these two values, -45° or 315°, they both represent the correct arguments).
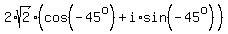So, the polar form of a complex number 2-2i is
2 - 2i =  .
It is the same as to say that the polar form of a complex number 2-2i is
2 - 2i =  .
In "cis"-form, it is the same as
2 - 2i =  =  .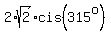
The modulus is ; the argument is -45° or 315° or any other number of degrees
which differs by a multiple of 360° from -45° or from 315°.
To make the argument unique, sometimes the conception of a PRINCIPAL ARGUMENT is used and the principal argument is taken:
it is the value of an argument in the range [0°,360°),
i.e. 315° in this problem.
----------------
On complex numbers, see introductory lessons
- Complex numbers and arithmetical operations on them
- Complex plane
- Addition and subtraction of complex numbers in complex plane
- Multiplication and division of complex numbers in complex plane
- Solved problems on taking roots of complex numbers
- Solved problems on arithmetic operations on complex numbers
- Solved problem on taking square root of complex number
- Solving polynomial equations in complex domain
- Miscellaneous problems on complex numbers
in this site.
Also, you have this free of charge online textbook on ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Complex numbers".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|
