Question 1198385: Three numbers A, B, C are in ratio a: b: c, if the following proportion is true:
A/a=B/b=C/c. If the angles of a triangle are in ratio 3: 4: 5, find the ratio of the corresponding sides
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Three numbers A, B, C are in ratio a: b: c, if the following proportion is true:
A/a=B/b=C/c. If the angles of a triangle are in ratio 3: 4: 5,
find the ratio of the corresponding sides
~~~~~~~~~~~~~~~~~~
If the angles of the triangle are in ratio A:B:C = 3:4:5, it means that
A = 3x, B = 4x, C = 5x, where x is the common measure.
Then 3x + 4x + 5x = = 180°, or 12x = 180°, which implies x = 180°/12 = 15°.
Hence, A = 45°, B = 60°, C = 75°.
Due to the sine law, it implies
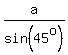 = = 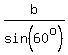 = = 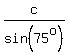 .
Thus the ratio of the corresponding sides is
a:b:c = sin(45°) : sin(60°) : sin(75°) = .
Thus the ratio of the corresponding sides is
a:b:c = sin(45°) : sin(60°) : sin(75°) =  : :  : : 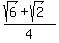 =
= =
=  : :  : : 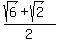 = 1.414 : 1.732 : 1.932 (rounded). ANSWER = 1.414 : 1.732 : 1.932 (rounded). ANSWER
Solved.
|
|
|