Question 1198347: Determine whether it is possible to draw a triangle
given each set of information. Sketch all possible
triangles where appropriate. Calculate, then label, all
side lengths to the nearest tenth of a centimetre and
all angles to the nearest degree.
b=12.2cm, c=8.2cm, AngleC=34
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Determine whether it is possible to draw a triangle
given each set of information. Sketch all possible
triangles where appropriate. Calculate, then label, all
side lengths to the nearest tenth of a centimetre and
all angles to the nearest degree.
b=12.2cm, c=8.2cm, AngleC=34
~~~~~~~~~~~~~~~~~~
Write the sine law identities
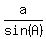 = = 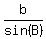 = = 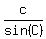 .
We have .
We have 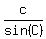 = = 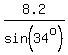 = = 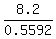 = 14.664.
So, = 14.664.
So, 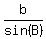 = 14.664, or sin(B) = = 14.664, or sin(B) = 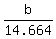 = = 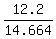 = 0.832 (rounded).
Since sin(B) is positive and less than 1, there are two possible values for the angle B measure.
You can find the measure of the angle B from sin(B) = 0.832 using your calculator (two possible values).
Doing this way, you will get two possible angles B,
and then you will get two possible angles C from A + B + C = 180 degrees
as C = 180 - A - B. = 0.832 (rounded).
Since sin(B) is positive and less than 1, there are two possible values for the angle B measure.
You can find the measure of the angle B from sin(B) = 0.832 using your calculator (two possible values).
Doing this way, you will get two possible angles B,
and then you will get two possible angles C from A + B + C = 180 degrees
as C = 180 - A - B.
At this point, I will stop my explanations.
The rest is just your job.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let's see if we can use the Law of Sines to determine angle B.
sin(B)/b = sin(C)/c
sin(B)/12.2 = sin(34)/8.2
sin(B) = 12.2*sin(34)/8.2
sin(B) = 0.8319699
B = arcsin(0.8319699) or B = 180-arcsin(0.8319699)
B = 56.3016 or B = 123.6984
These values are approximate.
If B = 56.3016, then
A+B+C = 180
A = 180-B-C
A = 180-56.3016-34
A = 89.6984
which is a valid angle measure since 0 < A < 180.
If B = 123.6984, then
A+B+C = 180
A = 180-B-C
A = 180-123.6984-34
A = 22.3016
which is also valid.
We have the SSA ambiguous case here, where we have 2 possible triangles.

Angle A could be 22.3016° marked in blue, or it could be 89.6984° marked in red.
B1 and B2 represent possible locations for point B.
Here's what it looks like to split the triangles up, to get a better look at them.

I've also erased the "1" and "2" from "B1" and "B2" respectively.
I'll let you use the law of sines to determine the missing side for each possible triangle.
I'll also let you round the angle measures to the nearest whole degree.
|
|
|