SOLUTION: Find (1+i*square root of 3)^8

Algebra ->  Trigonometry-basics -> SOLUTION: Find (1+i*square root of 3)^8      Log On


   

Question 1197764: Find (1+i*square root of 3)^8
Answer by ikleyn(52908) About Me  (Show Source):
You can put this solution on YOUR website!
.

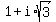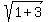The modulus of the number  1+%2B+i%2Asqrt%283%29  is sqrt%281%5E2+%2B+%28sqrt%283%29%29%5E2%29 = sqrt%281%2B3%29= sqrt%284%29 = 2.


The argument of this number is 60°  (because it is in QI and  tan(60°) = sqrt%283%29 ).


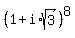Therefore, due to de Moivre formula,  %281+%2B+i%2Asqrt%283%29%29%5E8  has the modulus of  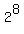2%5E8 = 256  and  the argument of  8*60° = 480°,

which geometrically is the same as 480° - 360° = 120°.



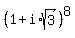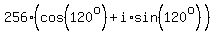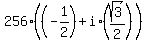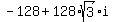Therefore,  %281+%2B+i%2Asqrt%283%29%29%5E8 = 256%2A%28cos%28120%5Eo%29+%2B+i%2Asin%28120%5Eo%29%29 = 256%2A%28%28-1%2F2%29+%2B+i%2A%28sqrt%283%29%2F2%29%29 = -128+%2B+128%2Asqrt%283%29%2Ai.    ANSWER

Solved, with explanations.