SOLUTION: sin^-1(2x√1-x^2)+sin^-1(3x -4x^3)=-pi/3 the value of x

Notice that due to the formula  sin(2a) = 2*sin(a)*cos(a),

you have  arcsin((2x*sqrt(1-x^2)) = 2a,  where  sin(a) = x.



Similarly, due to the formula  sin(3a) = 3*sin(a) - 4*sin^3(a),

you have  arcsin(3x-4x^3) = 3a,  where  sin(a) = x.



Therefore, the given equation

    sin^(-1)(2x*sqrt(1-x^2)) + sin^(-1)(3x -4x^3) = -pi/3


is equivalent to 

    2a + 3a = -pi/3,  where  sin(a) = x,

or

      5a    = -pi/3,   sin(a) = x,

       a    = 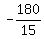 =  = -12°.



It implies  x = 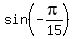.   It is the "exact" formula and the "exact" answer.



To get the numerical value, use your calculator or table of sinus: x = -0.20791169081... = -0.2079 (rounded).



CHECK.  2x*sqrt(1-x^2) = 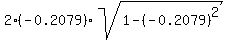 = -0.406715;  arcsin(-0.406715) = -0.418855117.

        3x -4x^3 = 3*(-0.2079) - 4*(-0.2079)^3 = -0.587756244; arcsin(-0.587756244) = -0.628282675.

        -0.418855117 - -0.628282675 = -1.047137791.


        From the other side, 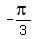  =  = -1.04719755.


        Both values,  -1.047137791  and  -1.04719755,  are close enough, confirming validity of the answer.