Question 1189322: If sinx-cosx= 1 /√3 , and sinx and cosx are the two roots to the equation 2x^2+px+q=0, the value of p^2- 8q would be
Answer by ikleyn(52906)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If sinx-cosx= 1 /√3 , and sinx and cosx are the two roots to the equation 2x^2+px+q=0,
the value of p^2- 8q would be
~~~~~~~~~~~~~~~
If sin(x) and cos(x) are the two roots of the equation 2x^2+px+q=0,
then due to Vieta's theorem
sin(x) + cos(x) = - , (1)
sin(x)*cos(x) = , (1)
sin(x)*cos(x) = 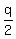 . (2)
Squaring equation (1) (both sides), it implies
sin^2(x) + 2sin(x)*cos(x) + cos^2(x) = . (2)
Squaring equation (1) (both sides), it implies
sin^2(x) + 2sin(x)*cos(x) + cos^2(x) = 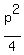 or
2sin(x)*cos(x) =
or
2sin(x)*cos(x) = 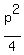 - -  ,
sin(x)*cos(x) = ,
sin(x)*cos(x) = 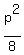 - - 
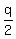 = = 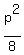 - -  p^2 = 4q + 4
p^2 - 8q = (4q +4) - 8q = -4q + 4. (3)
Next, from the other given equality,
sin(x) - cos(x) =
p^2 = 4q + 4
p^2 - 8q = (4q +4) - 8q = -4q + 4. (3)
Next, from the other given equality,
sin(x) - cos(x) =  .
Square both sides
sin^2(x) - 2sin(x)*cos(x) + cos^2(x) = .
Square both sides
sin^2(x) - 2sin(x)*cos(x) + cos^2(x) =  -2sin(x)*cos(x) =
-2sin(x)*cos(x) =  - 1 = - - 1 = - sin(x)*cos(x) =
sin(x)*cos(x) =  . (4)
Now from (1), (2), (3) and (4)
p^2 - 8q = -4q + 4 = -4*(2sin(x)*cos(x)) + 4 = . (4)
Now from (1), (2), (3) and (4)
p^2 - 8q = -4q + 4 = -4*(2sin(x)*cos(x)) + 4 = 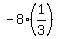 + 4 = 4 - + 4 = 4 -  = = 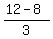 = =  .
ANSWER. Under given conditions, p^2 - 8q = .
ANSWER. Under given conditions, p^2 - 8q =  . .
Solved.
|
|
|