Question 1177441: r = 4 cos(6𝜃)
Identify zeros of r, 0 ≤ 𝜃 ≤ 2𝜋. Use a graphing utility to verify your results. (Enter your answers as a comma-separated list.)
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!

Identify zeros of  , ,
To find the zeros, set equal to zero and solve for theta. equal to zero and solve for theta.







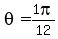




 intercepts: intercepts:
(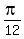 , , ),( ),( , , ),( ),(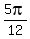 , , ),( ),( , , ),( ),( , , ),( ),(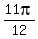 , , ),( ),(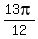 , , ),( ),( , , ),( ),(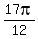 , , ) )

Answer by greenestamps(13215)   (Show Source): (Show Source):
|
|
|