Question 1177382: The three numbers (1/24)sinA, (1/3), and tan A are in geometric progression. Find the numerical value of cosA, where 0 degrees < A < 90 degrees. Should be solved without the use of a calculator.
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The three numbers (1/24)*sin(A), (1/3), and tan(A) are in geometric progression.
Find the numerical value of cos(A), where 0 degrees < A < 90 degrees. Should be solved without the use of a calculator.
~~~~~~~~~~~~~
Since the three terms (1/24)*sin(A), (1/3), and tan(A) form a GP, it implies that
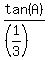 = = 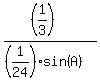 and hence
and hence
 = = 
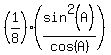 = =  3*(1-cos^2(A)) = 8*cos(A)
Introduce new variable x = cos(A) and write the last equation in the form
3 - 3x^2 = 8x
3x^2 + 8x - 3 = 0
3*(1-cos^2(A)) = 8*cos(A)
Introduce new variable x = cos(A) and write the last equation in the form
3 - 3x^2 = 8x
3x^2 + 8x - 3 = 0
 = = 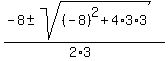 = = 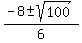 = =  .
So, one root is .
So, one root is  = = 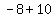 = = 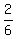 = =  , and it implies cos(A) = , and it implies cos(A) =  .
Another root is .
Another root is  = = 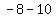 = = 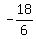 = -3, and it does not produce the corresponding cosine.
ANSWER. Under the given conditions, cos(A) = = -3, and it does not produce the corresponding cosine.
ANSWER. Under the given conditions, cos(A) =  . .
Solved (without using a calculator, as requested).
|
|
|