Question 1176031: Outside temperature over a day can be modeled as a sinusoidal function. Suppose you know the high temperature of 96 degrees occurs at 4 PM and the average temperature for the day is 85 degrees. Find the temperature, to the nearest degree, at 7 AM.
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Outside temperature over a day can be modeled as a sinusoidal function.
Suppose you know the high temperature of 96 degrees occurs at 4 PM and
the average temperature for the day is 85 degrees.
Find the temperature, to the nearest degree, at 7 AM.
~~~~~~~~~~~~~~~~~~~~~~
Our 24-hour cycle of the daily temperature change starts at 4 pm, when the temperature is maximal.
So, our sinusoidal function is, actually, the cosine function, if to start counting time from 4 pm = 16:00, or
T(t) = 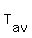 + + 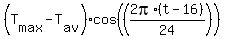 where "t" is the local astronomic time in the 24-hours "military" time scale in your watch.
At 7 am next day, we have
where "t" is the local astronomic time in the 24-hours "military" time scale in your watch.
At 7 am next day, we have 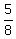 of the full cycle elapsed.
It corresponds to of the full cycle elapsed.
It corresponds to  on the unit circle, and on the unit circle, and 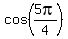 = - = -  .
So, the temperature at 7 am next day will be .
So, the temperature at 7 am next day will be
 = = 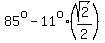 = 85° - 0.707*11° = 77.2°.
ANSWER. We can expect 77.2°, or 77° rounded at 7 am next day. = 85° - 0.707*11° = 77.2°.
ANSWER. We can expect 77.2°, or 77° rounded at 7 am next day.
Solved.
|
|
|