SOLUTION: Express cos(3a) in terms of cos⁡(a).

Algebra ->  Trigonometry-basics -> SOLUTION: Express cos(3a) in terms of cos⁡(a).       Log On


   

Question 1171119: Express cos(3a) in terms of cos⁡(a).
Answer by ikleyn(52756) About Me  (Show Source):
You can put this solution on YOUR website!
.
Express cos(3a) in terms of cos⁡(a).
~~~~~~~~~~~~~~~~


            There are several ways  (more than one unique way)  to derive this formula.

            I will show you here very elegant way using complex numbers. 


Let z be the complex number z = cos(a) + i*sin(a).

This complex number lies on the unit circle.


Raise the number to degree 3. Using de Moivre formula, you have

    z%5E3 = cos(3a) + i*sin(3a).   (1)


From the other side, applying the binomial expansion formula 

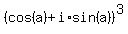    z%5E3 = %28cos%28a%29+%2B+i%2Asin%28a%29%29%5E3 =  = 

                             = .   (2)


In formulas (1) and (2), the left sidea are equal.  Hence, their right sides are equal.


Separating real and imaginary terms in formulas (1) and (2), we get the formula for  cos%283a%29


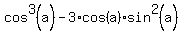    cos%283a%29 = cos%5E3%28a%29+-+3%2Acos%28a%29%2Asin%5E2%28a%29.    (3)


Substituting here  sin%5E2%28a%29 = 1+-+cos%5E2%28a%29,  you get from (3)


    cos%283a%29 = cos%5E3%28a%29+-+3cos%28a%29%2A%281-cos%5E2%28a%29%29 = 4cos%5E3%28a%29+-+3cos%28a%29.


It is the final formula  cos%283a%29 = 4cos%5E3%28a%29+-+3cos%28a%29.      ANSWER

Solved.