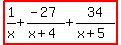Write the partial fraction decomposition of the following rational expression.
 The other person is WRONG!!
The other person is WRONG!!
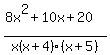 =
= 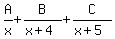
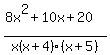 =
= 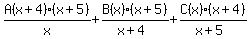 --- Multiplying right-side by LCD, x(x + 4)(x + 5)
--- Multiplying right-side by LCD, x(x + 4)(x + 5)
 --- Equating NUMERATORS, since DENOMINATORS are same
--- Equating NUMERATORS, since DENOMINATORS are same
 ------ Substituting - 5 for x, to determine the value of C
8(25) - 50 + 20 = 0 + 0 + C(- 5)(- 5 + 4)
200 - 50 + 20 = C(- 5)(- 1)
170 = 5C
------ Substituting - 5 for x, to determine the value of C
8(25) - 50 + 20 = 0 + 0 + C(- 5)(- 5 + 4)
200 - 50 + 20 = C(- 5)(- 1)
170 = 5C
 = 34 = C
= 34 = C

 ------ Substituting - 4 for x, to determine the value of B
8(16) - 40 + 20 = 0 + B(- 4)(- 4 + 5) + 0
128 - 40 + 20 = B(- 4)(1)
108 = - 4B
------ Substituting - 4 for x, to determine the value of B
8(16) - 40 + 20 = 0 + B(- 4)(- 4 + 5) + 0
128 - 40 + 20 = B(- 4)(1)
108 = - 4B
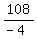 = - 27 = B
= - 27 = B

 ------ Substituting 1 for x, 34 for C, and - 27 for B, to determine the value of A
8(1) + 10 + 20 = A(5)(6) - 27(1)(6) + 34(1)(5)
8 + 10 + 20 = 30A - 162 + 170
38 = 30A + 8
38 - 8 = 30A
30 = 30A
------ Substituting 1 for x, 34 for C, and - 27 for B, to determine the value of A
8(1) + 10 + 20 = A(5)(6) - 27(1)(6) + 34(1)(5)
8 + 10 + 20 = 30A - 162 + 170
38 = 30A + 8
38 - 8 = 30A
30 = 30A
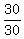 = 1 = A
So, (A, B, C) = (1, - 27, 34)
We then get:
= 1 = A
So, (A, B, C) = (1, - 27, 34)
We then get: 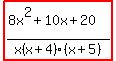 =
= 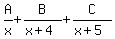 =
=