Question 1153915: Find the exact values of sin(2u),cos(2u),tan(2u)using the half-angle formulas.
sin u = -3/5, 0
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
(1) What does "sin u = -3/5, 0" mean?
(2) If you give use the values of sin u and cos u, we can't find the values of sin(2u), cos(2u), or tan(2u) using half-angle formulas -- we would need to use double-angle formulas.
If you want help with your questions, be careful to post them clearly and correctly.
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
(1) First, you should not use half-angle formulas.
(2) Second, for the given purposes, special formulas do exist in Trigonometry, that are called the double argument formulas.
These formulas are
 =  .
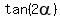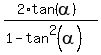(3) So, start calculating
 = +/-  = +/-  = +/-  = +/-  = +/-  .
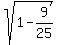Which sign to chose there, is the unknown fact - the problem does not provide a necessary info for it.
In this sense, your input is FATALLY incomplete.
(4) Having values of  and , you should substitute them into formulas for double arguments above,
and complete the assignment in this way.
--------------------
Again, the input is FATALLY INCOMPLETE; therefore, I can not continue.
The fact that the input is incomplete, is your FAULT.
and my conclusion is that the problem is presented in the post EXTREMELY UNPROFESSIONALLY.
|
|
|
