Question 1126640: Solve the given equation. (Enter your answers as a comma-separated list. Let k be any integer. Round terms to three decimal places where appropriate. If there is no solution, enter NO SOLUTION.)
(tan2(θ) − 16)(2 cos(θ) + 1) = 0
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13216)   (Show Source):
You can put this solution on YOUR website!
The product is 0 when either factor is 0.
---------------------------------------
skip these lines; I solved the wrong equation...
The second factor is 0 when cos(2x) = -1; the solutions are
2x = 2pi/3 +/- 2k(pi) --> x = pi/3 +/- k(pi)
or
2x = 4pi/3 +/- 2k(pi) --> x = 2pi/3 +/- k(pi)
-------------------------------------------
here is the corrected discussion of the second factor...
The second factor is 0 when 2cos(x) = -1, or cos(x) = -1/2. The solutions are
2pi/3 +/- 2k(pi)
or
4pi/3 +/- 2k(pi)
The first factor does not have exact zeros, the way the second one does. Its zeros are when
tan(2x) = 16
2x = arctan(16) +/- k(pi)
x = (1/2)arctan(16) +/-(k/2)(pi)
Use a calculator to get those zeros to the prescribed accuracy.
Answer by ikleyn(52943)  (Show Source):
You can put this solution on YOUR website! .
I'd like to make a couple of comments.
1. First, the analysis of the second factor by @greenestamps is incorrect.
The correct way to analyse it is THIS:
2*cos(x) + 1 = 0 is equivalent to
cos(x) = 
and has the solutions x = 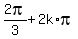 , k = 0, +/-1, +/-2, . . . and
x =  , k = 0, +/-1, +/-2, . . .
2. Regarding the first factor, I do not understand, what it represents:
(tan^2(x) - 16) (tan(x) in degree 2) or (tan(2x) - 16).
Probably, you are a novice in this forum.
If so, then please be accurate and attentive in writing your formulas.
Use properly parentheses and other mathematical symbols.
Otherwise, you will not get all possible benefits from this forum.
|
|
|
