Question 1122862: 1. Write a cosine function, f(x), such that on one period a local maximum is at (- pi/3, 1) followed by a local maximum at (2pi/3, -7). F(x)=
2. Write a tangent function, h(x), such that the halfway points on one period are (- pi/2, -2) and (pi/4, 4). H(x)=
3. Rewrite g(x)= 5cos (2x - pi/4) -3 as, k(x), a function of sine. I got: k(x)= 5sin (3 pi/4). Is it right?
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1. Clearly there can't be a local maximum at (-pi/3,1) and another at (2pi/3,-7). The maximum values have to be the same.
So I will assume that (2pi/3,-7) is the local minimum that follows the local maximum at (-pi/3,1).
We want a function in the form
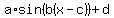
where a is the vertical stretch, b defines the period, c is the phase shift, and d is the vertical shift.
From the local maximum to the next local minimum is half a period; in this example that is from -pi/3 to 2pi/3, a difference of pi. That means the period of the function is 2pi; so there is no horizontal compression of the graph; b = 1.
The difference between the maximum and minimum values is 8, so the vertical stretch is 4: a = 4.
The center line is halfway between the maximum 1 and the minimum -7, at -3; d = -3.
The basic cosine function has its maximum at x = 0; since this function has its maximum at x = -pi/3, the phase shift is -pi/3: c = -pi/3.
We have all the pieces; the function with a=4, b=1, c=-pi/3, and d=-3 is

A graph, showing a local maximum at (-pi/3,1) and the following local minimum at (2pi/3,-7)...

2. We need a function in the form

where a is the vertical stretch, b defines the period, c is the phase shift, and d is the vertical shift.
The halfway points are (-pi/2,-2) and (pi/4,4).
The difference in x values between the halfway points is 3pi/4, so the period is 3pi/2. Since the period of the basic tangent function is pi, the graph is stretched horizontally by a factor of 3/2. That means b = (pi)/(3(pi)/2)) = 2/3.
The difference between the y values of the midpoints is 6. Since the difference between the y values at the midpoints of the basic tangent function is 2, the vertical stretch is 3: a = 3.
The center line is halfway between the y values at the midpoints, which is 1: d = 1.
The center of the period is halfway between the two midpoints, at x = -pi/8. Since the basic tangent function has the center of its period at x=0, the phase shift is -pi/8: b = -pi/8.
Again we have all the pieces. The tangent function with a=3, b=2/3, c=-pi/8, and d=1 is
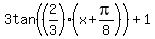
A graph, showing (-pi/2,-2) and (pi/4,4) as the halfway points of a period....

3. Your answer can't be right; the "2x" still has to be part of the argument for the sine function.
The given function is
5cos(2x-pi/4)-3
To find an equivalent sine function, you only need to know that cos(x) = sin(x+pi/2). Note that is easy to see if you see that the maximum value of the basic cosine function is at x = 0 while the maximum value of the basic sine function is at x = pi/2.
So all you need to do for this question is add pi/2 to the angle in the given formula:
5sin(2x+pi/4)-3
A graph of the two functions, with the sine function (green) shifted up 1 unit so you can see the two graphs...

|
|
|