SOLUTION: If secA=13/5 with A in quadrant 4 and tanB=-3/4 with B in quadrant 2, find the exact value of sin(A+B)

Algebra ->  Trigonometry-basics -> SOLUTION: If secA=13/5 with A in quadrant 4 and tanB=-3/4 with B in quadrant 2, find the exact value of sin(A+B)       Log On


   

Question 1117589: If secA=13/5 with A in quadrant 4 and tanB=-3/4 with B in quadrant 2, find the exact value of sin(A+B)

Found 2 solutions by solver91311, KMST:
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!














But













But



By similar analysis, . I'll leave the details in your capable hands. Then:



Congratulations. You have just won an all expenses paid trip to the land of "Do your own arithmetic."

John

My calculator said it, I believe it, that settles it

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
WHAT YOU NEED TO KNOW:
For any angle 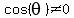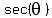theta , if cos%28theta%29%3C%3E0 , sec%28theta%29%22=%221%2Fcos%28theta%29 ,
and 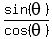tan%28theta%29%22=%22sin%28theta%29%2Fcos%28theta%29 .

For any angle theta , cos%28theta%29%2Bsin%28theta%29=1 .

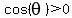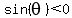If theta is in quadrant IV (four), cos%28theta%29%3E0 and sin%28theta%29%3C0 .

For any angles A 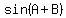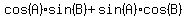and B , sin%28A%2BB%29%22=%22cos%28A%29sin%28B%29%2Bsin%28A%29cos%28B%29

WHAT COULD ALSO HELP:
Because teachers like problems with answers that are integer or rational numbers,
they often use right triangles with integer side lengths.
The three side length form what we call a Pythagorean triple,
like (3,4,5), (5,12,13), (8,15,17), or (7,24,25).
If you do not need to "show all of your work", those triangles save you time.
If you have to show all of your work, those triangles provide a good check.

For example, . For that theta in quadrant I, system%28cos%28theta%29=4%2F5%2Csin%28theta%29=3%2F5%2Ctan%28theta%29=3%2F4%29 .
The angle B from your problem, in quadrant II, has theta as its reference angle,
so system%28cos%28B%29=-4%2F5%2Csin%28B%29=3%2F5%2Ctan%28B%29=-3%2F4%29 .

Also, for A in quadrant IV, the reference angle is alpha shown below.
so system%28cos%28alpha%29=5%2F13%2Csin%28alpha%29=12%2F13%2Csec%28alpha%29=13%2F5%29 ,
so for A in quadrant IV, system%28cos%28A%29=5%2F13%2Csin%28A%29=-12%2F13%2Csec%28A%29=13%2F5%29 .