Question 1117559: Could someone give me some tips about how to solve this question ? I don't know how to do this question with decimals. Thanks you!
Give the smallest two solutions of cos(6θ) = 0.2771 on [ 0,2π ).
Separate the two solutions with a comma.
Be sure to round only once at the end.
Found 2 solutions by math_helper, ikleyn:
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! Could someone give me some tips about how to solve this question ? I don't know how to do this question with decimals. Thanks you!
Give the smallest two solutions of cos(6θ) = 0.2771 on [ 0,2π ).
Separate the two solutions with a comma.
Be sure to round only once at the end.
=======================================================
The last sentence needs to specify how many decimal places (which I'd expect to be 4 or less, because the value 0.2771 has 4 signficant digits). I will carry 7 decimal digits for all the calculations and you can round to the required number of digits.
Step-by-step:



Now, there are two solutions, the one above (in Q1), and  (in Q4). (in Q4).
This is because x is positive in Q1 and Q4, thus  has positive x in those two quadrants. I am referring to {{ 6* theta }}} here, finding has positive x in those two quadrants. I am referring to {{ 6* theta }}} here, finding 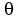 itself requires dividing by 6. itself requires dividing by 6.
Solving the two cases for  you should get you should get  rad for the Q1 angle and rad for the Q1 angle and  rad for the Q4 angle. rad for the Q4 angle.
A graph might help visualize this, where A and B are the approximate locations of the two solutions:

覧覧覧覧覧
EDIT 5/30/18:
In my post, I was referring to the quadrants of 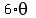 not not 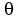 itself. For clarity, let itself. For clarity, let  then it was then it was 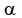 in Q1 and Q4. I did mention this fact and I apologize if it was not clear. in Q1 and Q4. I did mention this fact and I apologize if it was not clear.
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I'd like to make one notice (correction) to the solution by the tutor @Math_helper.
He correctly found one solution theta_1 = 0.215 radians in Q1.
He also correctly found the other solution theta_2 = 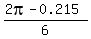 = 0.831 radians, but mistakenly referred to it as to the angle of Q4.
In fact, the angle theta_2 lies in Q1, too. = 0.831 radians, but mistakenly referred to it as to the angle of Q4.
In fact, the angle theta_2 lies in Q1, too.
|
|
|