Question 1114896: Given: cos (-105)
Find the exact value of the function without the use of a calculator.
I was unsure what to do with a negative, but from examples, I did the following where it "ignores" the negative.
cos (105) = cos (135 - 30)
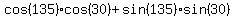
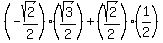
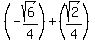
Final Answer: 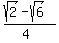
If the final answer is right, why does the (-) go away and if that procedure is incorrect how would you split up the -105? Thank you for any help!
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(53618)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
cos(a) = cos(-a) for any angle "a".
In particular, cos(-105°) = cos(105°), so your result is applicable to cos(-105°).
Your final result is RIGHT: cos(-105°) = 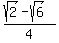 . .
Answer by MathTherapy(10719)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given: cos (-105)
Find the exact value of the function without the use of a calculator.
I was unsure what to do with a negative, but from examples, I did the following where it "ignores" the negative.
cos (105) = cos (135 - 30)
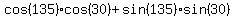
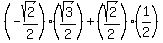
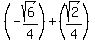 Final Answer:
Final Answer: 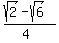 If the final answer is right, why does the (-) go away and if that procedure is incorrect how would you split up
the -105? Thank you for any help!
=================================
You're applying the DIFFERENCE of 2 angles here, which does give you
If the final answer is right, why does the (-) go away and if that procedure is incorrect how would you split up
the -105? Thank you for any help!
=================================
You're applying the DIFFERENCE of 2 angles here, which does give you
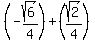 . However, the NEGATIVE is NOT IGNORED/does NOT just DISAPPEAR. . However, the NEGATIVE is NOT IGNORED/does NOT just DISAPPEAR.
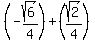 <==== You got up to this point <==== You got up to this point
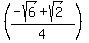 , which is EQUAL to, or the SAME as: , which is EQUAL to, or the SAME as: 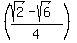 .
YOUR Final Answer: .
YOUR Final Answer: 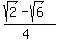 Looking at the 2 expressions ABOVE, one can clearly see that they're the SAME.
**Note:
You asked how the cos (- 105) could be SPLIT, if your answer is incorrect. Your answer isn't incorrect, as stated
above, but another SPLIT would be cos (- 105) = cos (- 60 - 45), or {cos [(- 60) + (- 45)]}, which would then
involve the SUM of 2 angles. Nonetheless, this yields the same result!
Looking at the 2 expressions ABOVE, one can clearly see that they're the SAME.
**Note:
You asked how the cos (- 105) could be SPLIT, if your answer is incorrect. Your answer isn't incorrect, as stated
above, but another SPLIT would be cos (- 105) = cos (- 60 - 45), or {cos [(- 60) + (- 45)]}, which would then
involve the SUM of 2 angles. Nonetheless, this yields the same result!
|
|
|