Question 1101623: Determine the values of
2θ (not θ) on [0,2π) that satisfy the following equation. (Separate multiple solutions with a comma. Give exact answers.)
3sin(2θ)=−3/√2
2θ=
You now have two equations representing all possible solutions for 2θ. Solve each of those equations for θ. (Let θ1 and θ2 represent the solutions on [0,2π), where θ1is less than θ2.)
θ1=
θ2=
Use these general solutions for θ to find the four solutions to 3sin(2θ)=−3/√2 on the intervall
[0,2π). (Separate multiple solutions with a comma. Give exact answers.)
θ=
Found 2 solutions by stanbon, ikleyn:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Determine the values of 2t (not t) on [0,2π) that satisfy the following equation. (Separate multiple solutions with a comma. Give exact answers.)
3sin(2t)=−3/√2
sin(2t) = -1/sqrt(2)
2t = 5pi/4 or 2t = 7pi/4
-----------------------------------------------------
You now have two equations representing all possible solutions for 2θ. Solve each of those equations for θ. (Let θ1 and θ2 represent the solutions on [0,2π), where θ1is less than θ2.)
t1= 5pi/8
t2= 7pi/8
--------------------------------
Cheers,
Stan H.
--------------
Use these general solutions for θ to find the four solutions to 3sin(2θ)=−3/√2 on the interval
[0,2π). (Separate multiple solutions with a comma. Give exact answers.)
θ=
Answer by ikleyn(52818)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
3*sin(2*a) = -3/sqrt(2)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Due to "typography" issues, I will replace  in my post by simple "a". in my post by simple "a".
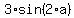 = =  (1) ====> (divide both sides by 3) ====> (1) ====> (divide both sides by 3) ====>
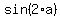 = = 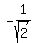 , or, which is the same, , or, which is the same,
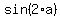 = =  .
It implies .
It implies 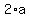 = =  or or 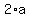 = =  .
Everything was simple to this point.
But in reality, accurate analysis only STARTS from this point.
1) It is obvious that .
Everything was simple to this point.
But in reality, accurate analysis only STARTS from this point.
1) It is obvious that 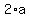 = =  implies implies  = = 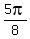 .
But if you stop here, you will loose another existing solution of the same family.
It is .
But if you stop here, you will loose another existing solution of the same family.
It is  = = 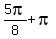 = =  .
Indeed, .
Indeed, 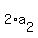 = = 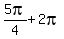 = = 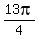 is GEOMETRICALLY the same angle as is GEOMETRICALLY the same angle as  and has the same value of sine,
so and has the same value of sine,
so  is the solution to the original equation (1), too.
Thus the relation is the solution to the original equation (1), too.
Thus the relation 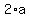 = =  creates and generates not one solution creates and generates not one solution 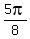 , but TWO solutions , but TWO solutions 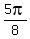 and and  of the same family. Notice, that they BOTH belong to the interval [0,
of the same family. Notice, that they BOTH belong to the interval [0, ).
2) The same or the similar story is with the solution ).
2) The same or the similar story is with the solution 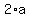 = =  .
It is obvious that .
It is obvious that 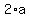 = =  implies implies  = = 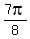 .
But if you stop here, you will loose another existing solution of the same family.
It is .
But if you stop here, you will loose another existing solution of the same family.
It is  = = 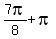 = = 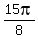 .
Indeed, .
Indeed, 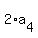 = = 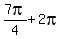 = =  is GEOMETRICALLY the same angle as is GEOMETRICALLY the same angle as  and has the same value of sine,
so and has the same value of sine,
so  is the solution to the original equation (1), too.
Thus the relation is the solution to the original equation (1), too.
Thus the relation 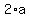 = =  creates and generates not one solution creates and generates not one solution 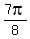 , but TWO solutions , but TWO solutions 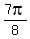 and and 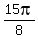 of the same family. Notice, that they BOTH belong to the interval [0,
of the same family. Notice, that they BOTH belong to the interval [0, ).
3. Thus the original equation (1) has 4 (four, FOUR) solutions in the interval [0, ).
3. Thus the original equation (1) has 4 (four, FOUR) solutions in the interval [0, ): ):
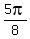 , ,  , , 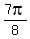 and and 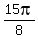 .
4. The plot below visually confirms existing of 4 solutions to the given equality: .
4. The plot below visually confirms existing of 4 solutions to the given equality:
 Plot y =
Plot y = 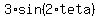 (red) and y = (red) and y =  (green) (green)
|
|
|