Question 1091300: 12. Kevin is riding a mini Ferris wheel. He reaches the maximum height of 9m at 5s and then reaches the minimum height of 1m at 65s.
a. What is the period (the length of time to complete one cycle)? b. What is the radius of the wheel?
c. Use the information given to sketch one cycle of the function. Label the graph.
d.the corresponding cosine equation
Answer by htmentor(1343)   (Show Source):
You can put this solution on YOUR website! a. He completes a half-cycle, from maximum to minimum height in 65 - 5 = 60s
Therefore the time to complete a full cycle, T = 120s
b. The diameter of the wheel is the max. height minus the min. height = 9 - 1 = 8m
Therefore the radius = 4m.
c. I'll leave this to you
d. The height at a time t can be modeled as:
 ,
where R is the radius of the wheel, T is the period, 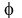 is the phase angle, and h0 is the height of the center of the wheel, i.e. the axis.
The height at any time t oscillates about the center height, h0 = 5, with an amplitude R = 4.
To find the phase angle, we note that the maximum height occurs at t = 5,
which means 
Putting it all together, the equation for the h(t) as a function of t is:
|
|
|
