SOLUTION: For sin a=-3/5 with terminal side in QIII and tan B=-5/12 with terminal side in QIV, find cos(a-B). multiple choice a. -33/65 b. -63/65 c. 63/65 d. 33/65

Draw a picture of the two given angles in their 
respective quadrants.  

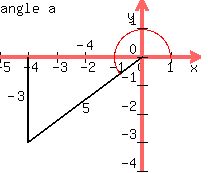
Since , make the opposite side
of the angle 'a' nearest the x-axis be the numerator of -3/5,
which is -3, and the hypotenuse be the denominator of -3/5,
which is 5.

Since , make the opposite side
of the angle 'B' nearest the x-axis be the numerator of -5/12,
which is -5, and the adjacent be the denominator of -5/12,
which is 12.  Use the Pythagorean theorem to calculate the 
adjacent side of angle 'a' to be -4 (negative because it goes
to the left.  Also use the Pythagorean theorem to calculate the 
hypotenuse of angle 'a' to be 13 (positive because the hypotenuse
is the TERMINAL SIDE of the angles which is ALWAYS taken positive.  

    

Now use an identity for 





   <--given


Substitute those values in



and simplify.  You finish.

Edwin