.
4sin^2x+sinx+3=6cos^2x
~~~~~~~~~~~~~~~~~~~~~~~~
 =
=  ---> (replace cos^2(x) by 1-sin^2(x)) --->
---> (replace cos^2(x) by 1-sin^2(x)) --->
 =
= 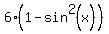 ,
,
 =
=  ,
,
 = 0.
Introduce new variable y = sin(x). Then the last equation takes the form
= 0.
Introduce new variable y = sin(x). Then the last equation takes the form
 = 0.
Its roots, according to the quadratic formula, are
= 0.
Its roots, according to the quadratic formula, are
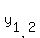 =
= 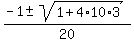 =
= 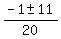 .
1.
.
1.  =
= 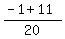 =
=  ---> sin(x) =
---> sin(x) =  ---> x =
---> x =  and/or x =
and/or x = 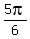 .
2.
.
2.  =
=  =
= 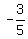 ---> sin(x) =
---> sin(x) = 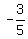 ---> x =
---> x =  and/or x =
and/or x =  .
Answer. The original equation has 4 solutions:
.
Answer. The original equation has 4 solutions:  ,
, 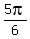 ,
,  and
and  .
.

Plot y =  (red) and y =
(red) and y =  (green)
(green)