It has no solutions because the least the left side ever gets is
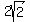 , which is about 2.828, when the left side is p/4, 3p/4, 5p/4, and 7p/4.
The largest it ever gets is 3, when x = 0, p/2, p, and 3p/2.
The left side can never equal 2. Thus there are no solutions.
Edwin
, which is about 2.828, when the left side is p/4, 3p/4, 5p/4, and 7p/4.
The largest it ever gets is 3, when x = 0, p/2, p, and 3p/2.
The left side can never equal 2. Thus there are no solutions.
Edwin