SOLUTION: If we change the circle from the standard unit circle to the circle with equation (x-2)^2+(y+5)^2=9 and we change the point Q(1,0) to be Q(4,√5-5). Define P(x,y) as before an

Algebra ->  Trigonometry-basics -> SOLUTION: If we change the circle from the standard unit circle to the circle with equation (x-2)^2+(y+5)^2=9 and we change the point Q(1,0) to be Q(4,√5-5). Define P(x,y) as before an      Log On


   

Question 1079474: If we change the circle from the standard unit circle to the circle with equation (x-2)^2+(y+5)^2=9 and we change the point Q(1,0) to be Q(4,√5-5). Define P(x,y) as before and let f(t)=x and g(t)=y.
a. Find equations for f(t) and g(t) as transformations of cos t and sin t.
b. Explain the significance of each of the attributes of the sinusoid functions in the previous part.
Confused. Can someone help me with this?
Thanks
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Is that the whole story? Or did we just walk in in the middle of the movie?
Is t an angle defined in some way?
It sound as if t is time, and you have a point P(x,y)
that started at some position
(maybe all the way to the right),
and is moving around the circle (maybe counterclockwise)
at some angular velocity (say w radians per second).
With all those assumptions (and t in seconds),
a point moving around the unit circle
would start at Q(1,0), and t seconds later its coordinates would be
x=cos%28wt%29 and y=sin%28wt%29 .
With some luck w=1, and it is just cos(t) and sin(t).
The new circle has center (2,-5) and radius 3 .
To make matters worse, the point would instead start
2 units to the right and sqrt%285%29 units up from the center,
at 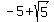%22Q+%28+4+%2C%22-5%2Bsqrt%285%29%22%29%22 .
That point has already moved an angle theta ,
with tan%28theta%29=sqrt%285%29%2F2
from the expected starting point,
which was all the way to the right of the circle center.
We have to add theta to the angle for sine and cosine,
and we have to account for the larger (3) radius.
After t seconds that point will be
3cos%28wt%2Btheta%29 to the right, and
3sin%28wt%2Btheta%29 up from the circle center, at
x=2%2B3cos%28wt%2Btheta%29 and y=-5%2B3sin%28wt%2Btheta%29 (or y=3sin%28wt%2Btheta%29-5 , if you do not want to start with a minus sign).
Maybe that would cover part a.

As for part b, I do not know what "attributes" were meant.
Different classes, different jargon, emphasis on different concepts/ideas.
Pick the words that resonate with your class experience.
The factor 3 is the highlight%28amplitude%29 of the sinusoidal functions.
It was changed from what you had in the unit circle,
"stretching" or "expanding" or "dilating" the functions vertically.
the theta added is a phase shift of the wave,
or horizontal translation of the function.
The 2 and -5 added to the functions for x and y
are vertical translations of the functions.
The period is 2pi%2Fw

EDIT:
If P has moved a distance t counterclockwise around a circle of radius 1 , centered at O(0,0),
the ray OP has swept an angle measuring t radians.
(In higher math we measure angles in radians, as if degrees are for elementary school only).
By convention, we consider counterclockwise sweeps as positive angles, clockwise sweeps as negative angles.
That way, we can say "do a 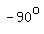-90%5Eo turn", meaning to turn right at the corner,
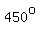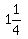or "give the knob a 450%5Eo turn," meaning to turn it 1%261%2F4 turns counterclockwise.
Then we define the trigonometric functions cos%28t%29=x and sin%28t%29=y
based on the coordinates of P.

If we use a circle with radius 3 and center C(2,-5),
for a point P(x,y) moving a distance t counterlockwise,
the ray CP would sweep an angle measuring t%2F3 radians.
Point 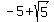%22Q+%28+4+%2C%22-5%2Bsqrt%285%29%22%29%22 is
4-2=2 units to the right, and
sqrt%285%29 units up from C(2,-5),
at 3 units distance from C, measured along a slanted line.
That line forms an angle theta with the horizontal, with cos%28theta%29=2%2F3 , which corresponds to about theta=0.841 , in radians.
Ray CQ would be a 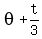theta%2Bt%2F3 counterclockwise sweep from (5,-5),
the point in the circle directly to the right of C.

We can write expressions for the new functions,
based on geometry:
With respect to C, Q would be
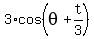3%2Acos%28theta%2Bt%2F3%29 units to the right, and
3%2Asin%28theta%2Bt%2F3%29 units up.
Its coordinates would be
x=2%2B3%2Acos%28theta%2Bt%2F3%29 , and y=-5%2B3%2Asin%28theta%2Bt%2F3%29 ,
so f%28t%29=2%2B3%2Acos%28theta%2Bt%2F3%29 and g%28t%29=-5%2B3%2Asin%28theta%2Bt%2F3%29 .
Those functions are sinusoidal functions with amplitude 3, and period 6pi . theta would be considered a phase shift.

You could also look at the new functions as transformations of the "parent" functions: cos(t) and sin(t) .
With respect to their parent functions,
f(t) and g(t) were
first "dilated" by a factor of 3 vertically and horizontally, because the circle was expanded by that factor.
There were 2 more changes after that, and I do not think the order matters.
The circle center was shifted 2 units right and 5 down,
shifting x=f%28t%29 2 units up, and shifting y=g%28t%295 units down.
Also the starting point was changed from (1,0) to Q,
shifting both functions to the right, because P was given a theta running start.
Those transformations are effected by the factors (dilations) , or added terms (shifts or translations).