SOLUTION: How do I find the exact value of the trigonometric expression given that cscU=-13/5 and cosV=3/4. How do I solve tan(V-U) using the given values?

Algebra ->  Trigonometry-basics -> SOLUTION: How do I find the exact value of the trigonometric expression given that cscU=-13/5 and cosV=3/4. How do I solve tan(V-U) using the given values?       Log On


   

Question 1074035: How do I find the exact value of the trigonometric expression given that cscU=-13/5 and cosV=3/4. How do I solve tan(V-U) using the given values?
Found 2 solutions by KMST, MathTherapy:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
You do not seen to have quite enough information listed.
With just the information you posted, the possibilities multiply, and you get 4 different answers.
If you had some clue that led you to the signs (positive or negative) of sin%28V%29 and cos%28U%29 ,
you could use the information given and trigonometric identities to find one answer.
That one answer may start as a cumbersome expression requiring simplification,
and ended as an ugly expression with square roots, but it would be the exact value.
Without more information there are 2 possible sin%28V%29 ,
and 2 possible cos%28U%29 , leading to 4 answers, and a lot more work.
By definition, csc%28U%29=1%2Fsin%28U%29 ,
so csc%28U%29=-13%2F5 means sin%28U%29=-5%2F13 .
Angle U could be in quadrant 3, with a negative cosine,
or in quadrant 4, with a positive cosine.
Either way, we know that for U (as for any angle)
cos%5E2%28U%29%2Bsin%5E2%28U%29=1 .
So, cos%5E2%28U%29=1-sin%5E2%28U%29=1-%28-5%2F13%29%5E2=1-25%2F169=%28169-25%29%2F169=144%2F169 ,
meaning that either cos%28U%5B4%5D%29=sqrt%28144%2F169%29=12%2F13 or cos%28U%5B3%5D%29=-sqrt%28144%2F169%29=-12%2F13 .
Similarly, from cos%28V%29=3%2F4 we can find
sin%5E2%28V%29=1-cos%5E2%28V%29=1-%283%2F4%29%5E2=1-9%2F16=7%2F16 , and
sin%28V%5B1%5D%29=sqrt%287%2F16%29=sqrt%287%29%2F4 for angle V%5B1%5D in quadrant 1,
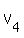or sin%28V%5B4%5D%29=-sqrt%287%2F16%29=-sqrt%287%29%2F4 for angle V%5B4%5D in quadrant 4.

There are "formulas" called trigonometric identities
that allow you to calculate the trigonometric functions of sums of angles, multiples of angles, and half of angles.
You can look them up online;
just search for "trigonometric identities" or "trig identities."
I see no point in memorizing most of those identities,
unless your teacher/instructor insists that you must memorize them.

For this particular problem, there are different ways to go about it.
1) You could use the trigonometric identities
sin%28A-B%29=sin%28A%29cos%28B%29-cos%28A%29sin%28B%29 , and/or
cos%28A-B%29=cos%28A%29cos%28B%29%2Bsin%28A%29sin%28B%29 .
to calculate 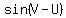sin%28V-U%29 and cos%28V-U%29 .
Then you could calculate tan%28V-U%29=sin%28V-U%29%2Fcos%28V-U%29 .
2) Alternatively, you could first calculate tan%28V%29=sin%28V%29%2Fcos%28V%29 and tan%28V%29=sin%28V%29%2Fcos%28V%29 ,
and use them along with trig identity
tan%28A-B%29=%28tan%28A%29-tan%28B%29%29%2F%281%2Btan%28A%29tan%28B%29%29 to calculate tan%28V-U%29 .

Option 1) looks more complicated
.
The four possibilities as to the signs (positive or negative) of sin%28V%29 and cos%28U%29 ,
leads to either a positive or negative sin%28V%29cos%28U%29
It could be if sin%28V%29cos%28U%29%3E0 ,
or otherwise.
For each of those sines, we could calculate two cosines as
cos%28X%29=sqrt%281-sin%5E2%28X%29%29 and cos%28X%29=-sqrt%281-sin%5E2%28X%29%29 .
If that looks ugly, you could calculate cos%28V-U%29 directly from the cos%28A-B%29 trig identity.
.
It could be .
It could be cos%28V%5B1%5D-U%5B4%5D%29=%2836-5sqrt%287%29%29%2F52 .
It could be cos%28V%5B1%5D-U%5B3%5D%29=-%2836%2B5sqrt%287%29%29%2F52=-%28cos%28V%5B4%5D-U%5B4%5D%29%29 .
It could be cos%28V%5B4%5D-U%5B3%5D%29=-%2836-5sqrt%287%29%29%2F52=-%28cos%28V%5B1%5D-U%5B4%5D%29%29 .
So, the four results are:

.

.




.

Option 2):
All the way at the top, we had
cos%28U%5B4%5D%29=12%2F13 or cos%28U%5B3%5D%29=-12%2F13 paired with sin%28U%29=-5%2F13
for the two possible U angles.
That makes tan%28U%5B4%5D%29=-5%2F12 or tan%28U%5B3%5D%29=%28-5%29%2F%28-12%29=5%2F12 .
All the way at the top, we had
sin%28V%5B1%5D%29=sqrt%287%29%2F4 or sin%28V%5B4%5D%29=-sqrt%287%29%2F4 paired with cos%28V%29=3%2F4 for the two possible V angles.
That makes tan%28V%5B1%5D%29=sqrt%287%29%2F3 or tan%28V%5B4%5D%29=-sqrt%287%29%2F3 .
Plugging those values into the trig identity
tan%28A-B%29=%28tan%28A%29-tan%28B%29%29%2F%281%2Btan%28A%29tan%28B%29%29 ,
we get





tan%28V%5B4%5D-U%5B4%5D%29=highlight%28-%28507sqrt%287%29-960%29%2F1121%29


... tan%28V%5B1%5D-U%5B4%5D%29=highlight%28%28507sqrt%287%29%2B960%29%2F1121%29

and since 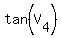tan%28V%5B4%5D%29 and tan%28U%5B3%5D%29 both are the opposites
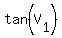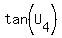of tan%28V%5B1%5D%29 and tan%28U%5B4%5D%29 respectively,

Answer by MathTherapy(10557) About Me  (Show Source):
You can put this solution on YOUR website!
How do I find the exact value of the trigonometric expression given that cscU=-13/5 and cosV=3/4. How do I solve tan(V-U) using the given values?
cos V is positive (> 0)

Since csc U is < 0, then sin U is also < 0

Thus, angles V and U are in the 4th quadrant

tan+%28V+-+U%29+=+%28tan+%28V%29+-+tan+%28U%29%29%2F%281+%2B+tan+%28V%29+%2A+tan+%28U%29%29



highlight_green%28matrix%281%2C3%2C+tan+%28V+-+U%29%2C+%22=%22%2C+-+9%2F20%29%29