.
8sinx - cosx = 4.
~~~~~~~~~~~~~~~~~~~~~~
Introduce new variable y = cos(x).
Then your equation becomes
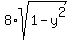 = 4 + y.
Square both sides.
64(1-y^2) = 16 + 8y + y^2,
65y^2 + 8y - 48 = 0.
= 4 + y.
Square both sides.
64(1-y^2) = 16 + 8y + y^2,
65y^2 + 8y - 48 = 0.
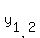 =
= 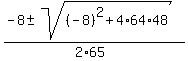 =
= 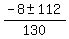 .
1.
.
1.  =
= 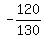 =
= 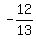 ---> cos(x) =
---> cos(x) = 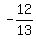 ---> x = +/-
---> x = +/- 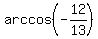 +
+  , k = 0, +/-1, +/-2, . . .
Check by substituting x into the original equation.
Only the solution in the second quadrant works: x = +
, k = 0, +/-1, +/-2, . . .
Check by substituting x into the original equation.
Only the solution in the second quadrant works: x = + 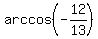 +
+  , k = 0, +/-1, +/-2, . . .
The solution in the third quadrant, x = -
, k = 0, +/-1, +/-2, . . .
The solution in the third quadrant, x = - 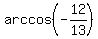 +
+  , k = 0, +/-1, +/-2, . . . doesn't work (is extraneous).
2.
, k = 0, +/-1, +/-2, . . . doesn't work (is extraneous).
2.  =
=  =
=  ---> cos(x) = {{4/5}}} ---> x = +/-
---> cos(x) = {{4/5}}} ---> x = +/- 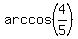 +
+  , k = 0, +/-1, +/-2, . . .
Check by substituting x into the original equation.
Only the solution in the first quadrant works: x = +
, k = 0, +/-1, +/-2, . . .
Check by substituting x into the original equation.
Only the solution in the first quadrant works: x = + 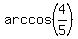 +
+  , k = 0, +/-1, +/-2, . . .
The solution in the fourth quadrant, x = -
, k = 0, +/-1, +/-2, . . .
The solution in the fourth quadrant, x = - 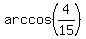 +
+  , k = 0, +/-1, +/-2, . . . doesn't work (is extraneous).
Answer. The solutions are these angles
, k = 0, +/-1, +/-2, . . . doesn't work (is extraneous).
Answer. The solutions are these angles
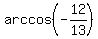 +
+  , k = 0, +/-1, +/-2, . . . and
, k = 0, +/-1, +/-2, . . . and 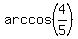 +
+  , k = 0, +/-1, +/-2, . . .
, k = 0, +/-1, +/-2, . . .

Plots y = 8sin(x) - cos(x) (red) and y = 4 (green)