Question 1069701: Suppose that the height h(t) (in meters) of a cabin of the London Eye as a function of the time t (in minutes) can be written as
h(t)=a + b * cos(c * t)
with a, b and c constants.
At time t=0 the cabin should start at the bottom. Use the data above to find the coefficients a, b and c. For c, work in radians. Give exact answers.
Below is the answer provided with my questions <<< INTERSPERSED >>>:
<<< I CAN'T VISUALIZE HOW COS COMES INTO THIS -- BY CONTRAST I THINK I COULD SEE USING SIN CAUSE = OPP/HYP, SO MULTIPLYING IT BY RADIUS (WHICH IS HYP) WOULD GIVE OPP, WHICH WOULD BE THE Y-COMPONENT OR THE DIFFERENCE OR ADDITION IN HEIGHT FROM OR TO THE HEIGHT OF THE AXIS>>>
It takes 30 minutes for a complete tour. This implies that 30* c = 2 * pi;
<<< IN 30 MIN. THEY TRAVEL ONE REVOLUTION OR 2 * PI. OK. BUT WHY DOES THIS MEAN THAT THE VALUE IN THE COS PARENTHESES HAS TO EQUAL THAT 2 * PI?
AND WHAT HAPPENED TO A & B ... WHAT IS THIS THOUGHT PROCESS THAT TAKES THE COS BY ITSELF? >>>
and therefore c= pi / 15.
So we have h(t)=a+b*cos((pi/15) * t).
Further we have
h(0)=0:a+b=0
and h(15)=135: a-b = 135.
This implies that
a = -b = 135/2
Found 3 solutions by KMST, Fombitz, rothauserc:
Answer by KMST(5330)   (Show Source): (Show Source):
You can put this solution on YOUR website! I read that the London Eye is 135 m tall and has a diameter of 120 m.
That tells me that the bottom is at a height of 15 m.
We need to find  , ,  , and , and  to make to make
 a good model for your height above the ground a good model for your height above the ground
 minutes after you start at the bottom. minutes after you start at the bottom.
WHY COSINE:
We would like  to be the start of the ride, to be the start of the ride,
where you probably are at the bottom at  , ,
and cosine maxes out at  , ,
where  . .
That works for  , ,
with  where where  . .
You could use sine, but 
would not make  the bottom height. the bottom height.
It would be the middle of the ride.
THE AMPLITUDE:
With  , the amplitude of , the amplitude of 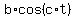 is is 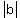 , ,
and  . .
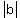 , the amplitude, , the amplitude,
is how far a cabin goes from the middle,
and that is half the diameter,
so  --> --> , ,
and  . .
THE HALF-WAY HEIGHT:
 is the height of the wheel hub. is the height of the wheel hub.
 , ,
and you go from 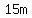 to to  and back and back
 . .
THE PERIOD:
Sine and cosine have a period of  . .
They reach their minimum only once every  . .
So if you start at the bottom at  , and , and
you return there for the first time at  minutes, minutes,
at  --> -->  . .
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! The London Eye is a ferris wheel, with h(t)= a + b * cos(c * t)
:
The London Eye has a diameter of 135 meters and passengers board a cabin when theta = 0 degrees at a height of 2 meters above the ground
:
The wheel has a radius of 135 / 2 = 67.5 meters so the height will oscillate about the center with amplitude of 67.5 meters
:
The center of the wheel must be at 67.5 + 2 = 69.5 meters so the midline of the oscillation will be at 69.5 meters
:
The wheel takes 30 minutes to complete one revolution so the height will oscillate with period 30 minutes
:
Since the rider boards at the lowest point, the height will start at the smallest value and increase, this follows the shape of a flipped cosine curve
:
Period is 30, so b = (2 * pi) / 30 = (pi / 15)
:
we could use a transformation of either the sine or cosine function, so
we look for characteristics that would make one function easier than
the other.
:
If we consider the graph of a cosine function that starts at the lowest height value, then
:
we want cosine function because it starts at either the highest or lowest value,
while a sine function starts at the middle value.
:
We know the cosine curve(in this case) was reflected because a standard cosine starts at the highest value, and this graph starts at the lowest value.
:
h(t) = -67.5 * cos( (pi/15) * t ) + 69.5
:
That should get you started to get the answer
:
|
|
|