Question 1066743: Solve for X when Sin(X)+cos(X)=0.4
I know the answer, but do not know how to answer it in an exam (without trial and error looking at a sin and cosine graph) (Please explain in degrees, not radians)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 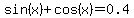
Let us square both sides of the equal sign.
The solutions of the resulting equation
will include all the solutions of the original equation,
and may include extra (extraneous) solutions,
but we can check at the end to eliminate the extraneous solutions.


Using the trigonometric identity  , ,
we can simplify the equation above to


Using the trigonometric identity  , ,
we can simplify the equation above to

Using the inverse function we find an approximate value for  : :
 (rounded). (rounded).
There are many other angles that have  . .
To begin with, for any angle  , ,  . .
Besides that, adding or subtracting any multiple of 
will give you a co-terminal angle with the same value for all its trigonometric functions.
So,  also has also has  , ,
and so do all  angles differing from angles differing from 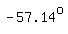 or or 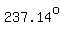 by a multiple of by a multiple of  . .
So, the solutions to the original equation would be among
 , ,  , ,  , ,  , ,
and other angles differing by a multiple of  . .
 and and  look like solutions, look like solutions,
and they check when substituted into the original equation.
So do all the angles differing from one of those solutions by multiples of  . .
On the other hand,
 with with 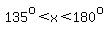 , and consequently , and consequently
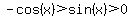 is obviously an extraneous solution, is obviously an extraneous solution,
since it will yield 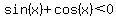 . .
So is  , with , with 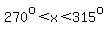 and and  . .
|
|
|