.
Write 5sin(t)-12cos(t) in the form of Asin(Bt+ϕ) using sum or difference formulas.
~~~~~~~~~~~~~~~~~~
First, 5sin(t) - 12cos(t) = 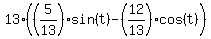 . (1)
Second, the angle
. (1)
Second, the angle 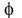 does exist such that
does exist such that 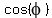 =
=  and
and 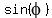 =
=  .
The rationality for it is the fact that
.
The rationality for it is the fact that 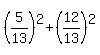 = 1.
You can easily check this identity keeping in mind that
= 1.
You can easily check this identity keeping in mind that 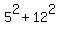 =
=  .
Now, you can write (re-write) the formula (1) as follows
5sin(t) - 12cos(t) =
.
Now, you can write (re-write) the formula (1) as follows
5sin(t) - 12cos(t) = 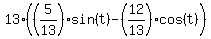 =
= 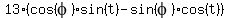 =
= 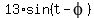 .
Thus we presented 5sin(t) - 12cos(t) in the form
.
Thus we presented 5sin(t) - 12cos(t) in the form 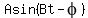 with A = 13, B = 1, and
with A = 13, B = 1, and 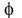 =
= 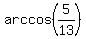 =
= 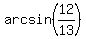 .
.
Solved.