.
Find the maximum and minimum values of each given function and state the corresponding values of x. ( 0 <= x < 2pi )
(1) 
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Take the derivative on "x": y'(x) = -sin(x) + 2*(-sin(x/2)*(1/2) = - sin(x) - sin(x/2).
Equate it to zero. You will get an equation
-sin(x) - sin(x/2) = 0, or
2*sin(x/2)*cos(x/2) + sin(x/2) = 0, or ( after factoring )
sin(x/2)*(2*cos(x/2) + 1) = 0.
It deploys in two independent equations
1. sin(x/2) = 0 ---> x/2 = 0, 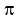 ,
,  ---> x = 0 and x =
---> x = 0 and x =  ( the only roots in the segment [
( the only roots in the segment [ ,
, ] ).
2. 2*cos(x/2) + 1 = 0 ---> cos(x/2) =
] ).
2. 2*cos(x/2) + 1 = 0 ---> cos(x/2) =  ---> x/2 =
---> x/2 =  ,
, 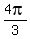 ---> x =
---> x = 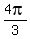 ( the only root in the segment [
( the only root in the segment [ ,
, ] ).
Answer:
a) Maximum at x = 0: 3.
b) Minimum at x =
] ).
Answer:
a) Maximum at x = 0: 3.
b) Minimum at x = 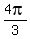 :
: 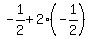 = -1.5.
c) Local maximum at x =
= -1.5.
c) Local maximum at x =  : 1 + 2*(-1) = -1.
: 1 + 2*(-1) = -1.
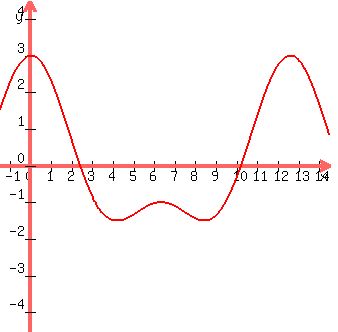
Plot y = cos(x)+2cos(x/2)
|