.
A rhombus of side 12 cm has two angles of 60 degree. Calculate the lengths of the diagonals of the rhombus.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Apply the Law of Cosines.
The shorter diagonal
We work with the isosceles acute triangle whose lateral sides are 12 cm long and the angle between them is 60°.
= 
= 
= 
= 12 cm.
As you see, the shorter diagonal has the length of 12 cm, same as the two other sides of this triangle,
so the triangle is equilateral, actually.
We could foresee it, since the isosceles triangle with one (any) angle of 60° is equiangular and equilateral.
The longer diagonal
We work with the isosceles obtuse triangle whose lateral sides are 12 cm long and the angle between them is 120°.
= 
= 
= 
= 
= 
cm.
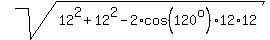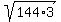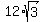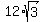Answer. The diagonals of the rhombus are 12 cm and cm.
