Question 1016640: Write expressions that give all solutions to the following equation. (Express your answers in degrees. Let k be any integer. Enter your answers as a comma-separated list.)
cos θ/2 − cos θ = 1
Note: I have tried using the half-angle formal and squared boy sides to get rid of the square root. After that i found common denominators and did the algebraic stuff. I got 60, 180, and 300. I let k be an integer of 360k for each, but it was wrong. Thank you!
Answer by ikleyn(52905)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Write expressions that give all solutions to the following equation. (Express your answers in degrees. Let k be any integer. Enter your answers as a comma-separated list.)
cos θ/2 − cos θ = 1
----------------------------------------------------------
 = =  . (1)
For me, it is easier to introduce new variable . (1)
For me, it is easier to introduce new variable  = = 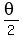 and to solve an equation for and to solve an equation for 
 - -  = =  . (2)
Surely, you know that . (2)
Surely, you know that  = = 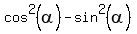 = =  .
Substitute it into (2). You will get .
Substitute it into (2). You will get
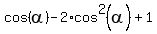 = =  , or , or
 = =  , ,
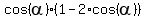 = =  .
Thus you have two separate equations
1. .
Thus you have two separate equations
1.  = 0 ---> = 0 --->  = =  ---> --->  = = 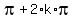 , k = 0, +/-1, +/-2, . . .
2. , k = 0, +/-1, +/-2, . . .
2. 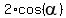 = =  ---> --->  = =  ---> --->  = +/- = +/-  + +  ---> --->  = +/- = +/- + +  , k = 0, +/-1, +/-2, . . . , k = 0, +/-1, +/-2, . . .
|
|
|