Question 1014764: Analyze the function f(x) = sec 2x. Include:
- Domain and range
- Period and Amplitude
- Two Vertical Asymptotes
Answer by ikleyn(53538)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Analyze the function f(x) = sec 2x. Include:
- Domain and range
- Period and Amplitude
- Two Vertical Asymptotes
----------------------------------------------
f(x) = sec(2x) = 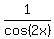 . .
The domain is all number line (all real numbers) except those where cos(2x) = 0.
These exceptional values are 2x =  , k = 0, =/-1, +/-2, . . . , k = 0, =/-1, +/-2, . . .
In other words, the exceptional values for x are 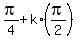 , k = 0, =/-1, +/-2, . . . , k = 0, =/-1, +/-2, . . .
The range is the union of two infinite intervals: y <= -1 and y >=1.
The period is the same as for the function cos(2x), i.e.  . .
There is no amplitude. The conception/notion of an amplitude is not applicable to the function y = sec(2x).
Vertical asymptotes are there where cos(2x) = 0, i.e. at the points 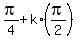 , k = 0, =/-1, +/-2, . . . - the same exceptional points mentioned above. , k = 0, =/-1, +/-2, . . . - the same exceptional points mentioned above.
Plot of the function y = sec(2x) is shown below.
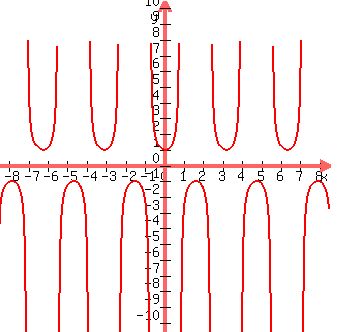
Figure. Plot y = sec(2x)
|
|
|
|