Question 1009676: Find all solutions in the interval [0, 2π). (Enter your answers as a comma-separated list.)
sin(θ) cos(3θ) + cos(θ) sin(3θ) = 0
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Solve
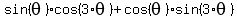 = =  . .
--------------------------------------------------------------------
Use the formula
sin(alpha)*cos(beta) + cos(alpha)*sin(beta) = sin(alpha+beta)
It is the formula for sine of the sum of arguments - one of fundamental formula of Trigonometry.
See, for example, the lesson Addition and subtraction formulas in this site.
When you apply this formula to the left side of your equation, you will get
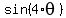 = =  . .
The general solution is 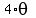 = =  , k = 0, +/-1, +/-2, . . . , k = 0, +/-1, +/-2, . . .
Hence,  = = 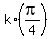 , k = 0, +/-1, +/-2, . . . , k = 0, +/-1, +/-2, . . .
For the given interval [ , ,  ) the solutions are ) the solutions are 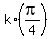 for k = 0, 1, 2, . . . , 7. for k = 0, 1, 2, . . . , 7.
|
|
|