Question 1008002: Please help me solve this problem:
Use the function f(x)=sin(x)+cos(x), where 0≤x≤π , to answer the following:
1. Determine all stationary points. Classify the points as relative minima or maxima.
2. Locate any points of inflection.
3. Determine the endpoints of the interval and sketch the graph.
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Use the function f(x)=sin(x)+cos(x), where 0 =< x <=  , to answer the following:
1. Determine all stationary points. Classify the points as relative minima or maxima.
----------------------------------------------------------------
If you want to solve it as a Calculus problem, then take a derivative of the function
f'(x) = cos(x) - sin(x)
and equal it to zero. The stationary points are the roots of this equation:
f'(x) = 0, or cos(x) - sin(x) = 0.
This equation is the same as cos(x) = sin(x) or 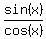 = 1 = tan(x).
Hence, x =  is the only stationary point in the interval 0 =< x <= .
To classify further if x = is the maxima or minima, you should take the second derivative of the original function
f''(x) = -sin(x) - cos(x)
and evaluate its sign at this point. You have
f''() =  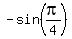-  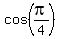=  -  =  < 0.
Then Calculus says that x = is the maxima.
So this part of the claim is solved.
The plot of the function is below:
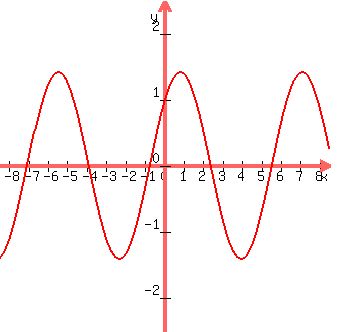Figure. Plot sin(x) + cos(x)
|
Actually, it is shifted and scaled sine wave, or sinusoid.
You can prove it using Trigonometry, and this fact opens the way to trigonometry analysis of the function.
But it is just another theme, although closely related to the first one.
|
|
|
