|
This Lesson (PROOF OF THE LAW OF COSINES) was created by by Theo(13342)   About Theo:
This lesson provides an overview of the Proof of the Law Of Cosines.
REFERENCES http://www.clarku.edu/~djoyce/trig/laws.html http://mathproofs.blogspot.com/2006/06/law-of-cosines.html http://www.mathamazement.com/Lessons/Pre-Calculus/06_Additional-Topics-in-Trigonometry/law-of-cosines.html http://www.themathpage.com/aTrig/law-of-cosines.htm http://pages.pacificcoast.net/~cazelais/173/law-sines-cosines.pdf http://pballew.net/lawofcos.htm http://www.kkuniyuk.com/M1410602.pdf There are 3 cases to the proof. They are: CASE 1 All angles in the triangle are acute. CASE 2 There is one right angle in the triangle. CASE 3 There is one obtuse angle in the triangle. LAW OF COSINES EQUATIONS They are: The proof will be for: This is based on the assumption that, if we can prove that equation, we can prove the other equations as well because the only difference is in the labeling of the points on the same triangle. PROOF OF LAW OF COSINES EQUATION CASE 1 All angles in the triangle are acute. A picture of our triangle is shown below: 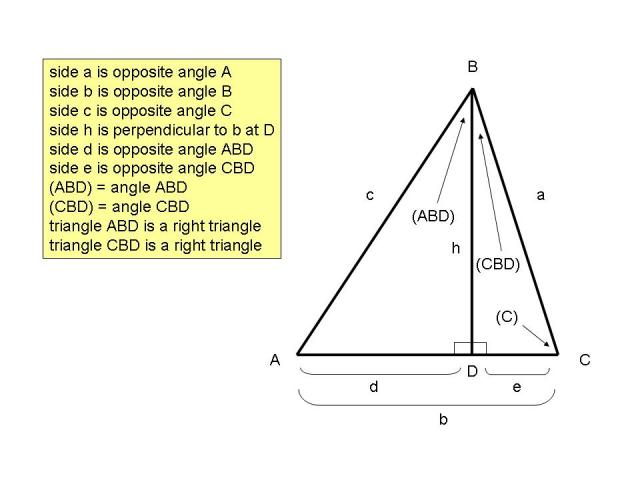 Our triangle is triangle ABC. We drop a perpendicular from point B to intersect with side AC at point D. That creates 2 right triangles (ABD and CBD). Side b from triangle ABC is equal to side d from triangle ABD plus side e from triangle CBD. Since Triangle ABD and CBD are both right triangles, we can use the Pythagorean Formula to identify the relationship between the hypotenuse and each leg of each triangle. For Triangle ABD, we get: ***** means this is the equation that will eventually be equal to Since b = d + e, this means that d = b - e. Substituting in our equation, we get: Since we also know that sin(C) in Triangle CBD = h = a*sin(C). We can substitute for h in our equation to get: Since If we complete the squaring of (b-e), then it becomes If we plug this into our equation, then we get: Since we know that cos(C) in Triangle CBD is equal to If we substitute for e in our equation, then we get: Since Since we know that b*a is the same as a*b, then we can rearrange terms in our equation to get: We can factor out the Since we know that cos2(C) + sin2(C) = 1, then we get If we substitute By rearranging terms, this becomes the same as: Since this is exactly the same as the original equation we were trying to prove, then we are done. This concludes the proof for Case 1. CASE 2 There is one right angle in the triangle. This makes it a right triangle. In a right triangle, the Pythagorean Formula prevails. We start off with our original equation of Since c is the hypotenuse of this right triangle, then angle C is opposite side c and is equal to 90 degrees. If angle C is equal to 90 degrees, then cos(C) = cos(90) = 0. This makes 2*a*b*cos(C) equal to 0. The equation The picture of our right triangle is shown below: 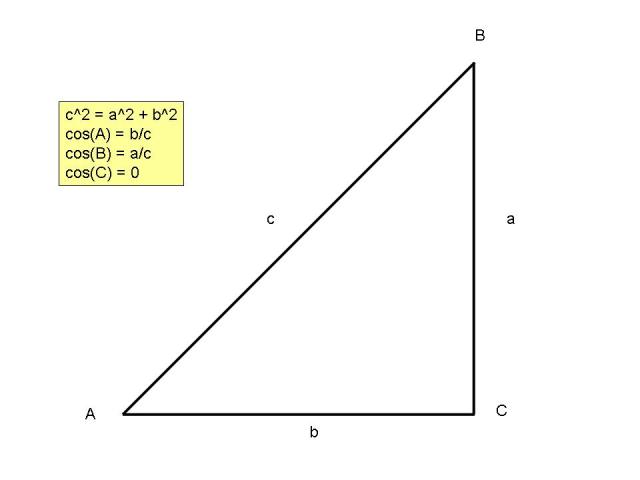 Since the Pythagorean formula prevails in a right triangle, and the Pythagorean Formula is a special case of our original equation, then we are done. This concludes the proof for case 2. CASE 3 There is one obtuse angle in the triangle. In this proof, angle C is the obtuse angle. We drop a perpendicular from point B to intersect with the extension of side b at point D. A picture of our triangle is shown below:  We are trying to prove that: We start off with ***** means that this is the equation that will eventually become This is from the well known Pythagorean Formula of Our c = Pythagoras' c Our e = Pythagoras' a Our h = Pythagoras' b  From our diagram, we can see that: From that, we get We can substitute in our equation of Since we know that the sine of the supplement of an angle is the same as the sine of the angle, we can substitute (C) for (BCD) to get: Since we know that Since we can see from the diagram that Since we know that Since we know that Since we know that the cosine of the supplement of an angle equals minus the cosine of the angle, we can substitute -cos(C) for cos(BCD) to get: Since we know that Since we know that We can re-arrange the terms in our equation to get: Since this is exactly the same as our original equation that we are trying to prove, then we are done. This concludes the proof for Case 3. Questions and Comments may be referred to me via email at |